Dokumendid > Keemia > Füüsikaline > Füüsikalised uurimismeetodid - KT II kordamine

Röntgendifraktsioon

Braggi võrrandist: mõõtes ära θ ja teades lainepikkust, saame kindlaks teha d ja seeläbi identifitseerida kristallsturktuuri. Kindlad aatomid mõjutavad difrageerunud kiire faasi ja mitte sarnased aatomid kindlates positsioonides võivad põhjustada kindlate difraktsioonipiikide puudumist. On olemas suur andmebaas erinevate difraktsioonimustritega, mis lubab enamikku ühendeid identifitseerida vastavalt difraktsiooni asukohtadele ja intensiivsustele

1. Millisele seadusele baseerub röntgendifraktsiooni meetod (valemi tuletus skeemi põhjal), tuua see seos lihtsustatud kujul;

Paralleelne x-ray kimp A-D-I langeb aatomtasandile nurga all θ_hkl ning peegeldub neilt sama nurga all. Kiir A hajub aatomily B ja kiir D aatomilt F. Peegeldunud kiired peavad täitma konstruktiivse interferentsi tingimusi, st nende faasid peavad kokku langema. Selleks peab nende optiliste teepikkuste erinevus olema täisarvkordne lainepikkus.

BE ja BG on joonistatud langevate kiirtega risti, seega kahelt naabertasandilt peegeldunud kiirte vahel tekib optiline teepikkus vahega EF+FG, EF=FG=d_hklsin θ_hkl. Siit järeldub ka Braggi valem nλ=2 d_hklsin θ_hkl.

Kui Braggi valemis n=1, on tegu 1st järku peegeldusega ja n=2 puhul teist järku peegeldusega tasandilt hkl. Kui n=2, siis 2λ=2 d_hklsin θ_hkl -> λ=2 (d_hkl/2) sin θ_hkl, mis kirjeldab esimest järku peegeldust tasanditelt interplanaarsete kaugustega d_hkl/2. Tasandite parv interplanaarsete kaugustega d_hkl/2 omab Milleri indekseid 2h2k2l,mistõttu 1st järku peegeldus tasanditelt 2h2k2l on eristamatu 2st järku peegeldusest tasanditelt hkl. Seetõttu lihtsustatud Braggi valemi võib kirjutada kujul: λ=2 d_hklsin θ_hkl

defineerida reaalne ja pöördvõre

Otsene kristallvõre

defineeritud läbi aatomtasandite, mida kirjeldavad indeksid h, k, l ja ühikrakud.

Aatomtasandid, mis on paralleelsed tasandiga h, k, l moodustavad parve indeksitega nh, nk, nl (n=1, 2, 3, .. ), kus tasandite vahekaugus on d_hkl/n.

Pöördvõre

Otsese võre igale tasandile vastab pöördvõre teatud punkt.

Seejuures konstrueeritakse pöördvõre kindla kristallivõre jaoks, tõmmates sirge läbi koordinaatide alguspunkti nii, et see oleks risti vastavate tasanditega h, k, l.

Selle joone pikkus on d*_h,k,l=1/d_h,k,l.

Seejuures vastavad pöördvõre punktid parve nh, nk, nl tasanditele, mis kõik annavad ühesuguse panuse difraktsiooni.

Seega määrab pöördvõre teatud hulga potentsiaalsete võresõlmede difraktsioonipildi.

Samas, kui antud sümmeetriaga võre puhul difraktsioon mingilt tasandilt on keelatud, siis puudub vastav võresõlm ka pöördvõres ja vastupidi, teatud “karakteristliku” difraktsioonimaksimumide puudumise järgi saab määrata kristallvõre tüübi.

Pöördvõre – võre, mis asub pöördruumis. Igale võretasandile vastab pöördvõres üks punkt, punkt on seotud sellega, et punkt sellel tasandil läheb mingisse kindlasse punkti ruumis. Pöördvõre punkt asub sellise vektori tipus, mis on selle tasandiga risti; pöördvõrdeline tasanditevahelise kaugusega.

loetleda Bravais võred

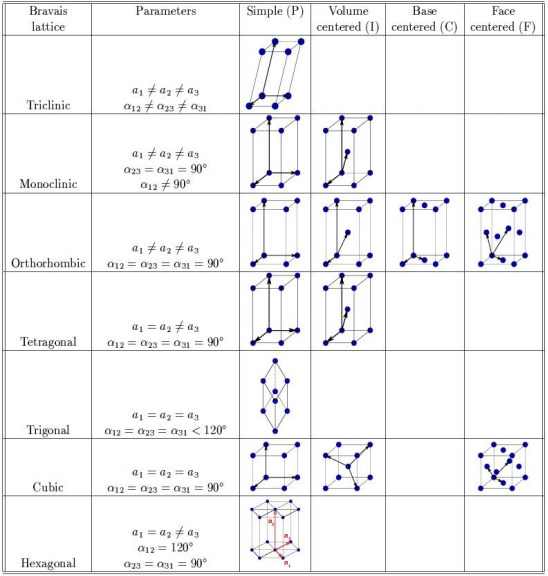
defineerida aatomtasandid ja nende kirjeldamise viis.

Aatomtasand on tasand, kus sõlmpunktides asuvad aatomid on asetatud perioodiliselt. Aatomtasandiks on vähemalt 3 mitte-kollineaarset aatomit sisaldav tasand. Kirjeldatakse täisarvuliste Milleri indeksitega h, k, l. Tasandiga h, k, l paralleelsed olevad aatomtasandid moodustavad parve, mida tähistatakse indeksitega nh,nk,nl ( n=1,2,3…), kus tasandite vahekaugus on /n.

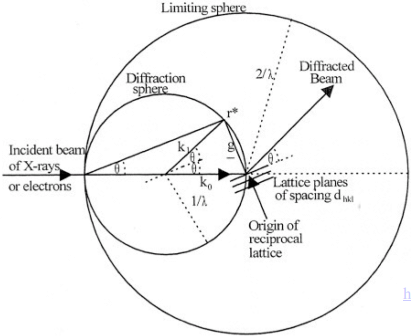
Mida kujutab Ewaldi sfäär, tuua skeem ja vektorvõrrand koos seletustega.

Ewaldi sfäär

saab ennustada röntgenkiire/osakese difraktsiooni suunda pöördvõres konstrueerides vastava sfääri

primaarkiir läbib koordinaatide alguspunkti nii reaal- kui ka pöördvõres

konstrueeritakse sfäär raadiusega R=1/λ (λ - kiirguse lainepikkus) nii, et selle keskpunkt asuks primaarkiire joonel ning asuks koordinaatide alguspunktist kaugusel R

sel juhul puudutab sfäär koordinaatide alguspunkti

difraktsioon leiab aset, kui sfäär läbib pöördvõre sõlme

difrageerunud kiire suuna määrab k₁ alguspunktiga Ewaldi sfääri keskelt ja lõpp-punktiga r*_h,k,l, kus see sfäär lõikab pöördvõre sõlme

seega määratakse difraktsioonitasandid pöördvõre sõlmedega r*_h,k,l, mis rahuldavad vektorvõrrandit: g=k₁-k₀

g-pöördvõre vektor, vastab difraktsiooni tasandile

k₀ ja k₁ vastavalt algse ja difrageerunud kiirguse lainevektorid

Difraktsioon toimub pöördvõre sõlmedes kui pööratakse monokristalli või polükristalli (pulbri) puhul, kus difraktsioonis osalevad erinevates suundades orienteeritud võretasandite parved korraga. Ükski pöördvõre sõlm väljaspool sfääri raadiusega 2R (keskpunkt koordinaatide alguspunktis) ei läbi Ewaldi sfääri, ega võta osa difraktsioonist. Seega on tegu limiteeriva sfääriga.

2. Selgitada millest sõltub röntgenkiirguse hajumisreflekside/-joonte intensiivsus, baseerudes elektroni hajumisel elektronidelt, aatomilt/molekulilt ja ühikrakult.

Hajumine elektronidelt

X-ray on elektromagnetiline laine, mis interakteerub tugevasti elektronidega, hajudes sellelt kas koherentselt või mittekoherentselt.

Koherentse hajumise korral kiire esialgne lainepikkus interaktsioonil ei muutu , toimub vaid võnkumise faasimuutus, mis on võrdne λ/2π.

See faasimuutus on sama ka elektronide difraktsiooni puhul, millest järeldub, et elektron hajutab röntgenkiirt intensiivsusega I₀ nii, et emiteerunud kiirguse intensiivsus I suunas 2θ, kaugusel r elektronist, mille laeng on e ja mass M, avaldub seosega (c – valguskiirgus):

I = I_0 \frac{e^4}{r^2{M}^2{c}^4} {\sin }^2 2 \theta

Mittekoherentne, e. Comptoni hajumine tekib, kui röntgenkvant põrkudes elektroniga kaotab energiat koguses hv, nii et hajunud kiire lainepikkus suureneb võrreldes pealelangenud kiire lainepikkusega:

\mathrm{h\nu } = E = \mathrm{hc} / \lambda

kuna primaar- ja mittekoherentselt hajunud röntgenkiirte faaside vahel puudub kindel sõltuvus, siis see efekt suurendab lihtsalt fooni.

Hajumine aatomitelt

Kiirguse hajumine toimub nii tuumalt kui elektronidelt, kuid arvestades väga suurt masside vahet elektroni ja aatomituuma vahel ning rakendades seost g=k₁-k₀ näeme, et tuumadelt hajumise võime jätta arvestamata.

Seega on hajumine aatomilt määratud peamiselt hajumisega aatomi elektronkatete elektrondielt.

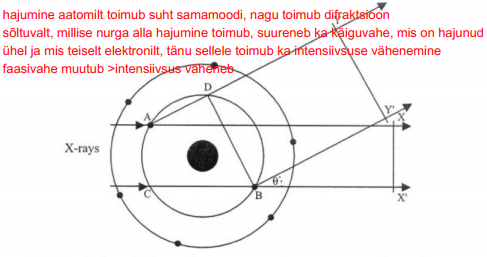
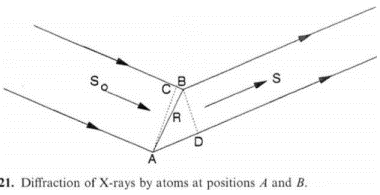
Nagu jooniselt näha, kuna aatomi mõõtmed on lõplikud, siis kiired, mis hajuvad elektronidelt positsioonides A ja B läbivad erineva teepikkuse, enne kui jõuavad tasandile YY’. Nende kiirte jaoks, mis hajuvad samas suunas primaarkiirega ja mis jõuavad tasandile xx’ faasivahe = 0 (on faasis), kuna nad läbivad ühesuguse summaarse teepikkuse enne ja pärast hajumist.

Kui difraktsiooninurk suureneb, suureneb ka käiguvahe CB-AD kiirtele, mis hajuvad elektronidel A ja B ja millega kaasneb ühtlasi summaarse laine amplituudi vähenemine tasandilt YY’. Summaarselt iseloomustab kiirguse hajumist aatomilt elektronide tihedusjaotus. Seejuures primaarkiire lühem lainepikkus põhjustab suurema amplituudi vähenemise.

Hajumise efektiivsus aatomilt kindlas suunas iseloomustab suurus f, mida nimetatakse hajumisfaktoriks:

f = \frac{\mathrm{aatomi\; poolt\; hajutatud\; laine\; amplituud}}{\mathrm{elektroni\; poolt\; hajutatud\; laine\; amplituud}}

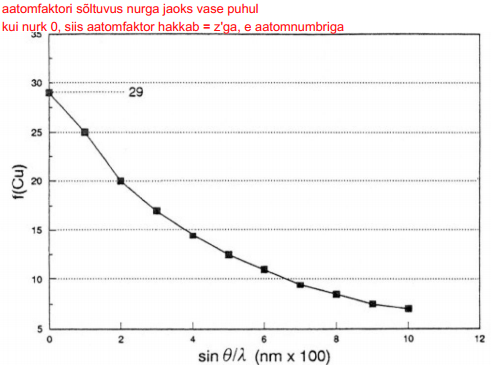
Kuna f on võrdne elektronide arvuga aatomis, kui hajumisnurk θ=0, seega sel juhul f=Z. Kuid üldiselt f väärtus väheneb kui θ suureneb ja/või λ väheneb (graafik Cu jaoks)

Hajumine ühikrakult

Vaatleme ühikraku aatomite mõju hajunud kiire intensiivsusele. Kuna ühikrakk on väikseim korduv võre ehituselement, siis on see ühtlasi viimane aste hajunud kiire intensiivsuse määramisel. Situatsioon on sarnane kiirte hajumisega aatomi erinevates punktides asuvatelt elektronidelt, kuid nüüd tekivad faasierinevused seetõttu, et aatomid asuvad ühikraku erinevates sõlmedes. Olgu aatom A koordinaatide algpunktis ja B punktis u,v,w (aatomitevahelised koordinaadid), siis aatomitelt B ja A suunas h,k,l hajunud lainete faasivahe on:

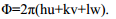(intensiisvus alati võrdne amplituudi ruuduga)

Kui aatomid on ühesugused (sama element), siis iga aatomi poolt hajutatud laine amplituud on võrdne; kui aga aatomid kuuluvad erinevatele elementidele (erinev Z), siis tuleb lõppintensiivsuse saamiseks kombineerida erinevate lainete amplituudid ja faasid.

Hajunud laine amplituudi saab kirjeldada komplekse eksponentfunktsiooniga Ae^iΦ ja intensiivsust selle amplituudi ruuduga, |Ae^iΦ|²; amplituud on aga võrdne faktori f väärtusega, kui hajumine toimub vaadeldavalt aatomilt. Seega:

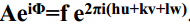
Hajumine ühikrakult: piikide intensiivsus

Piikide suhtelise intensiivsuse määramiseks on vaja teada proportsinaalsustegurit seoses

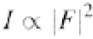. (F – struktuurifaktor, summaarse laine amplituud hajumisel ühikrakult)

Need tegurid sõltuvad katse läbiviimise viisist. Näiteks monokristalli uurimisel kasutatakse valget röntgenkiirgust, mis katab pidevalt teatud lainepikkuste vahemiku, ja siin lähevad otsesed arvutused keerukaks, mida viiakse läbi harva. Nende meetodite puhul, kus kasutatakse monokromaatset röntgenkiirgust, näiteks pulbermeetod, tuleb lisaks struktuurifaktorile arvesse võtta veel 5-t faktorit:

(Struktuurifaktor)

Lorentsi,

polarisatsiooni,

multiplitseerimise

neeldumise ja

temperatuuri faktoreid.

Tavaline on vaadelda Lorentsi ja polarisatsioonifaktorit koos. X-ray allikas tekitab polariseerimata kiire, kuid Võnkuvad aatomid kristallis ei hajuta polariseerimata kiirgust ühtlaselt kõikides suundades. Tekib osaliselt polariseeritud difrageerunud kiir, mille intensiivsuse kadu on

.

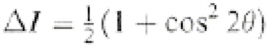Lisaks mõjutab analüüsi aeg ja difraktsiooni ulatus. Nende kombineerimisel saame Lorentsi polarisatsiooni faktori

.

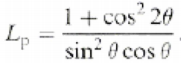See faktor vähendab difrageerunud röntgenkiirguse intensiivsust keskmistel väärtustel.

Multiplitseerimisfaktor (p) kujutab endast difraktsiooni piiki tekitavate aatomtasandite arvu.

Neeldumisfaktor (A()) on seotud kiirguse neeldumisega objekti läbides.

Mingi kindla paksusega objekti läbiv röntgenkiire intensiivsus sõltub neeldumistegurist. (neeldumisf.)

Temperatuuriefekt – soojusvibratsioonid põhjustavad aatomi suurenemist, avaldub hajumisfaktori f muutuses (väheneb, mida suuremad vibratsioonid)

Defineerida hajumisfaktor ja struktuurifaktor;

Hajumisfaktor (vt ka graafik ülevalt)

Hajumise efektivsus aatomilt kindlas suunas iseloomustab suurus f, mida nimetatakse hajumisfaktoriks:

f=aatomi poolt hajutatud laine amplituud/elektroni poolt hajutatud laine amplituud.

Kuna f on võrdne elektronide arvuga aatomis, kui hajumisnurk θ=0, seega sel juhul f=Z. Kuid üldiselt f väärtus väheneb kui θ suureneb ja/või λ väheneb

Struktuurifaktor

Ühikrakult hajunud laine on üksikutelt aatomitelt hajunud lainete summa, ja selle summaarse laine amplituudi nimetatakse struktuurifaktoriks, F. See on lainete amplituudidega A1, A2, A3,... ja faasinurkadega Φ1, Φ2, Φ3,… summa üle ühikraku.

Kui kujutada iga laine amplituudi lainevektori pikkusega ja faasi selle vektori suunaga, saab hajunud kiirt kujutada lainevektorite summana (vt. skeem allpool). Seega j-ndalt aatomilt hajunud laine saab lahutada horisontaalseks ja vertikaalseks vektori pikkuse komponendiks, vastavalt fjcos Φj ja fjsin Φj.

Nende komponentide summa joonistab kolmnurga, mille hüpotenuusiks on F, kus |F|2 võrdub laine intensiivsusega. Struktuurifaktor näitab, kas difraktsioon mingilt aatomtasandilt on olemas, või mitte.

Valemid:

Saadud valem lihtsustub, kui võtta arvesse ühikraku (kristallivõre) sümmeetria. Nii, on tsentersümmeetriliste võrede (näit. ruumtsentreeritud, kuid mitte CsCl võre) puhul võrrandi teine liige null, kuna sin 2π=0.

Lihtsama sümmeetriaga kristallide sagedamini vaadeldavate tasandite jaoks saab tingimused, kas difraktsioon antud tasandilt eksisteerib või mitte, jälgides lihtsat arutelu:

primitiivse kuubilise kristalli kõik tahud hajutavad.

Ruumtsentreeritud kuubilise kristallis toimub hajumine, kui h+k+l on paarisarvuline täisarv, kuid mitte siis, kui on paaritu täisarv;

tahktsentreeritud võre korral kui h, k ja l on kõik ühte tüüpi (paaris või paaritud), siis hajumine leiab aset,

segatüübi korral ei leia aset.

tuua näited konkreetsete suure sümmeetriaga kristallstruktuuridega.

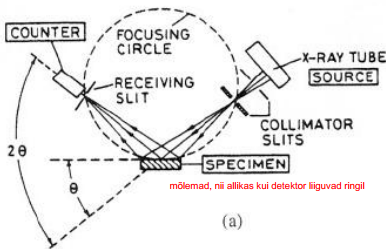
3. Selgitada pulberdifraktomeetria mõõteskeemid a) klassikalisel kujul ja b) difraktomeetrit kasutades.

a) klassikaline kuju

Fikseeritud λ, muutuv θ:

Peeneks uhmerdatud kristalliline pulber koosneb suurest hulgast väikestest kristallidest, kristalliitidest, mis on üksteise suhtes juhuslikult orienteeritud.

Kui selline pulber asetada monokromaatse röntgenkiirguse teele, siis kiirgus hajub kindlates suundades, millistes on täidetud Braggi valemi tingimused.

Need suunad moodustavad koonilised pinnad mille ühises tipus asub väike hajutav prooviobjekt.

(Lorenzi faktor: koonused, mis väiksema difraktsiooninurga alla, nendest läheb pilusuuruste avaga palju rohkem kiirgust läbi, kui laiematest koonustest; Kui meil on mingi pulber, siis otse vaadatuna (st küljelt), siis pole vahet, difraktsiooni saame nii ehk nii, mida suuremaks nurga ajame, seda kõrgemaks läheb teisipidi orienteeritud tasandilt tuleva kiirguse osakaal; kui aatomite hulk väiksem, siis sellest kohast ka difrageerunud kiirguse intensiivus väiksem.)

(a) röntgenkiirguse koonus-hajumistasandid pulberobjektilt, mille tipu poolnurk on n2θ, ja (b) Debye-Scherrer pulberdifraktsiooni fotograafiline mõõteskeem, milles prooviobjekt pöörleb ümber röntgenkimbu suunalise telje ja difraktsioonikaared (hajumiskoonuste lõiked) jäädvustatakse fotofilmi rõngale, mis on mässitud kaamera siseküljele. Kasutades teadaolevat kaamera raadiust ja mõõtes filmil difraktsioonijoonte asukoha kauguse väljuva kiirtekimbu keskkpunktist, saab arvutada iga difraktsioonijoonele vastava hajumisnurga 2θ ja sellele vastavate aatomtasandite vahelise kauguse d_hkl.

b) difraktomeetrit kasutades

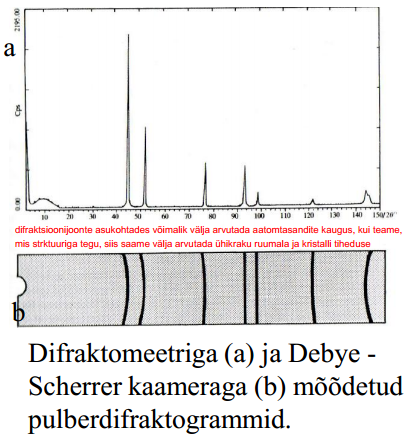Pulberdifraktsiooni reflekside mõõtmine toimub kaasajal automaatsete goniomeetriliste difraktomeetrite abil. Siin mõõdetakse reflekside intensiivsus ja hajumisnurk 2θ stsintillatsioondetektori abil. Lahutusvõime on difraktomeetritel suurem, kui fotofilmil, kuna objektid toimivad peeglitena, aidates refokuseerida hajunud kiirgust. Loomulikult registreeritakse hajumisandmed arvutisse; viimane juhib ka kogu suhteliselt pikaajalist mõõtetsüklit.

Kuidas aitavad puuduvad refleksid määrata polükristalliliste ainete kristallstruktuuri, tuua mõni näide.

Kindlatel kuubilistel kristallidel on suuruse 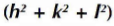kindlad väärtused, kus refleksid olemas või puuduvad. 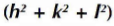suuruse erinevatele väärtustele vastavad kindlad h,k,l kombinatsioonid. Näiteks suurusel 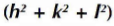on väärtus 3 primitiivse ja tahktsentreeritud kuubilise struktuuri korral, puudub aga ruumtsentreerituse korral. Vastav h,k,l kombinatsioon oleks 1,1,1. Konkreetsed tingimused on indeksitega h,k,l ära määratud, mille korral refleksid ilmnevad. Näiteks ruumtsentreerituse korral peab kehtima tingimus .

Kuidas arvutatakse difraktsiooni andmete alusel kristallilise aine tihedus, näiteks NaCl, CsCl, KCl.

Kuubilise ühikraku ruumala V saab arvutada võreparameetri abil. Teades osakeste arvu, saab massi, saab arvutada tiheduse: 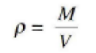. Peab arvestama, et nurkades ja äärtes asuvad osakesed kuuluvad korraga mitmele ühikrakule korraga.

Tõlge kristallitiheduse saab kindlaks teha valmistades vedelike segu, milles kristallid on lahutsumatud (kristallid ei hõlju pinnal ega vaju põhja): sellisel juhul kristallil sama tihedus vedelikuga. Vedeliku tiheduse saab kindlaks määrata kasutades nn tiheduspudelit.

Mis on difraktomeetrias faasianalüüs ja kuidas see käib.

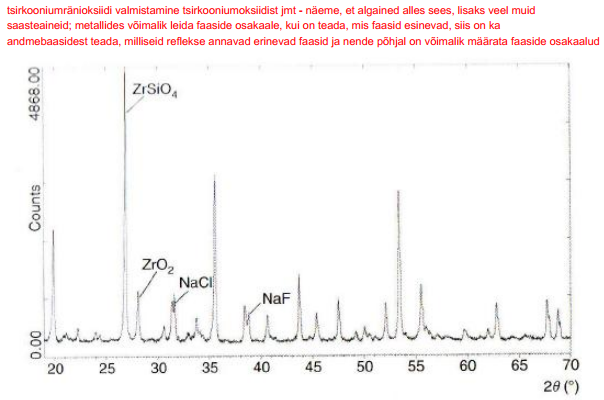
Tundmatute faaside määramine on raske (kuid mitte võimatu), kuna väiksema sümmeetriaga kristallid annavad palju reflekse, mis viib difraktsioonijoonte kattumisele ja seega raskendab või teeb võimatuks reflekside indekseerimise ja nende intensiivsuse mõõtmise.

Praktikas kasutatakse tuntud koostisega proovide difraktogrammide andmebaasi (näit. Joint Committee for Powder Diffraction Standards, JCPDS), mille difraktogramme võrreldakse tundmatu proovi omaga.

Selline difraktogrammide “sobitus” tehakse arvutiprogrammide abil ja seega on võimalik kasutada mahukaid järjest täiendatavaid andmebaase.

Siiski saab pulberdifraktsioonimeetodit kasutada vaid proovide kvalitatiivseks analüüsiks, ja seda tehakse edukalt nt väikeste kristallide segude määramisel geoloogilistes objektides.

Samas saab aine puhtust selle meetodiga määrata vaid ligikaudselt, kuna pulberdifraktsioon ei ole võimeline detekteerima amorfseid komponente, ega lisandeid, mille sisaldus on väiksem kui ~5%.

Samas saab pulberdifraktsiooniga hästi määrata, kas kaks lähedast ainet, milles nt üks metall asendab teist, on isomorfse struktuuriga või mitte.

Kuidas määratakse polükristalliliste ainete kristalliitide suurust? Selgitada lauegrammide saamise skeeme.

Kui kristalliidi suurus väheneb, laieneb difraktsioonijoon. Teoreetiliselt peaksid difrageeruvad kiired mõlemal pool Braggi nurka andma mittekonstruktiivse interferentsi, ja seega difraktsioonijoon olema terav. Suuremate kristalliitide korral see ka nii on, ja siin toimub summeerimine üle paljude aatomtasandite difrageerunud kiirte. Kui kristalliitide suurus üha väheneb, tekib olukord, kus kristalliidis pole piisavalt aatomtasandeid, et Braggi nurgast väiksel hälbimisel toimuks täielik destruktiivne interferents, ja seega difraktsioonijoon laieneb.

Debay-Scherreri valem võimaldab määrata kristalliitide suuruse difraktsioonijoone laiuse abil, kui:

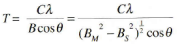
Kus, T on kristalliitide paksus, λ on röntgenkiirguse lainepikkus (T ja λ omavad samu ühikuid), θ on Braggi nurk, ja B on difraktsioonijoone poollaius (the fullwidth at half-maximum, FWHM), mis on korrigeeritud seadmest tingitud joone laienemise osas (B_M ja B_S on vastavalt objekti ja standardi difraktsioonijoone poollaiused).

Kristallide suurus määratakse antud hajumissuuna jaoks.

(Saab kasutada ka kihtide paksuse määramiseks, kuid praktikas kasutatakse pigem röntgenpeegelduse (XRR) meetodit)

Laue meetod:

Kiirguse difraktsioonvõre periood peab olema samas suurusjärgus kiirguse lainepikkusega. Kalgi röntgenkiirguse jaoks on selliseks difraktsioonivõreks kristallilise aine ruumiline, perioodiline kristallvõre, kus aatomtasandite vaheline kaugus on suurusjärgus 10-1000 pm.

Fikseeritud nurk θ, muutuv lainepikkus, λ:

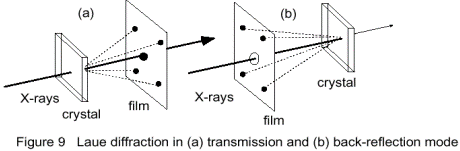Üks võimalus rahuldada Braggi seadust on kiiritada paigalasuvat monokristalli polükromaatse (“valge”) röntgenkiirgusega, mida genereerib näit. röntgentoru. Sel juhul koosneb kiirguse spekter karakteersetest joontest ning pidevast kiirgusest, mis katab teatud lainepikkuste vahemiku, ja seega kiiritatakse kristalli samaaegselt erinevat lainepikkust omava kiirgusega. Paigalasuva monokristalli puhul on selle aatomtasandid ruumis fikseeritud. Iga kristallvõre aatomtasandite parv peegeldab (hajutab) teatud lainepikkusega kiirgust, kindlate hajumisnurkade, θ_hkl, suundades, mis rahuldavad Braggi seost. Kristallvõrelt hajunud (difrageerunud) kiired saab detekteerida kas fotoplaadil, või kaasajal üha rohkem kasutatavatel elektroonilistel kujutismaatriksitel, näit. CCD-kaameratega. See asetatakse kas õhema objekti taha, skeem (a) või selle ette, skeem (b - enamlevinud), mis fikseerivad, vastavalt, läbinud või tagasipeegeldunud röntgenkiired.

Tuleb silmas pidada, et Laue-reflekside järgi saame määrata küll kiirguse hajumisnurgad θ, kuid ei saa määrata selles suunas hajunud kiirguse lainepikkust, λ. Seega ei saa seda tehnikat kasutada kristallvõre võrekonstandi määramiseks. Samas saab selle tehnika abil orienteerida kristalli kindla aatomkihi (kristalli tahu) suunas.

Probleemküsimused:

1. Kas pulbermeetodiga saab määrata tabletiks kokkupressitud peene kristallilise materjali kristallstruktuuri (põhjenda)?

2. Mis on kristallilise aine röntgentihedus ja kuidas seda määratakse?

3. Kas difraktsiooni meetodiga saab määrata kristallilise materjali paisumiskoefitsienti ja kuidas?

4. Kas ka osakesi saab kasutada tahkise struktuuri uuringuteks – mille alusel ja milliseid?

Aatomjõu mikroskoopia

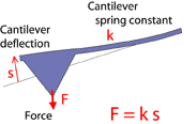
4. Selgitada Hooke seadust ja kus seda kasutatakse AFM puhul.

Vedrukonsooli painutamiseks vajaminevat jõudu kirjeldab Hooke‘i seadus:

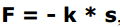
kus jõud F sõltub lineaarselt painutuse suurusest, s ja tegur k iseloomustab vedru elastsust, nim. vedru elastsusteguriks või vedrukonstandiks.

Turul saadaolevate vedrukeste elastsustegurid varieeruvad 4-ja suurusjärgu ulatuses – samuti ka jõu suurus, mis nad avaldavad objektile.

Millised põhilised jõud mõjuvad teraviku tipu ja pinna aatomite vahel?

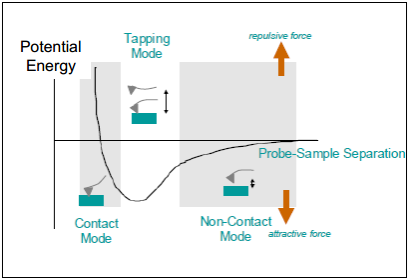Teraviku lähendamisel puhtale tahkise pinnale hakkavad teatud kaugusel teraviku tipu ja pinna aatomite vahel mõjuma van der Waalsi tõmbejõud (1-20 nN):

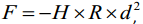
H- materjalist sõltuv konstant, R- tipu radius, d- tipu ja pinna vaheline kaugus.

Tipu edasisel lähenemisel pinnale hakkavad prevaleerima lähidistantsilised elektrostaatilised tõukejõud.

Vedrukese resonantsi võnkesagedus sõltub vedru elastsuskonstandist k ja vedrukese massist m:

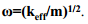
Valemis on k asemel k_eff, kuna k väärtus muutub tipu ja pinna vastastikmõju tõttu nende lähenemisel. Kui ΔF tähistab jõu laplasiaani, avaldub k_eff:

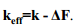
Toodud valemid näitavad, et kui tipp liigub objekti pinna poole, kus jõu gradient suureneb ja on positiivne (vt.joonist eelmisel slaidil), siis ka vastav laplasiaan on positiivne, ja k_eff ning ω vähenevad. Viimane tähendab resonantsipiigi nihkumist väiksemate sageduste poole.

Kirjeldada optilise detekteerimisega aatomjõu mikroskoobi tööpõhimõtet seadme skeemi abil.

Millised on AFM tööviisid, selgita tööpõhimõtet.

Töörežiimid:

Konstantse kõrguse puhul skaneerimise jooksul skanner ei muuda oma pikkust ning kujutis saadakse konsooli paindumisest ehk fotodetektori signaalist. (Kasutatakse aatomlahutuse saamiseks). Sellega vaadeldakse atomaarselt siledaid pindu, mille puhul vedrukese painded ja seega ka jõud on väikesed ning ei tekita objektis märgatavaid deformatsioone.

Konstantse jõu töörežiimil (realiseeritakse tagasiside süsteemi sisselülitamise abil) hoitakse konsooli paine konstantsena ja kontrollitakse skanneri Z-liikumist. Sellisel juhul saadakse kujutis registreerides piesoskanneri pikkust reguleerivat pinget. Meenutus: STM korral konstantne voolu töörežiim

Tööviisid

Mittekontakne tööviis, dünaamiline:

teravik vibreerib konstantse sagedusega (vedrukese resonantssageduse lähedal, tüüpiliselt 50-400 kHz) amplituudiga 20-100 nm (2-10 nm ?; esimene Maido konsp, teine mitte), objekti pinnast mõne nanomeetrise kaugusel. Kuna ideaalsel juhul teravik ei puuduta kunagi objekti pinda, saab selle tööviisiga uurida “pehmeid” ja “kleepuvaid” materjale ning ei toimu objekti ega teraviku mustumist.

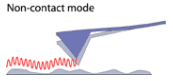
Nt saab uurida: teibi liimiv pind

Puutekontaktne töövis, dünaamiline:

Teravik objektile mõnevõrra lähemal ja võngub veidi suurema amplituudiga, nii et oma trajektoori madalaimas punktis korraks puudutab objekti.

Lisaks topograafilisele pildile registreeritakse ka amplituudi või faasipilt. Faasipilt kirjeldab nihet või faasi viivitust, mis tekib jõusensori võnkumisel objekti pinna kohal. Pinna heterogeensetel aladel on see viivitus erinev . Seega võib faasipilt olla kontrastsem kui topopilt.

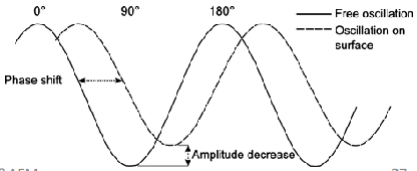
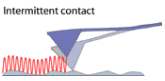
Mõlema dünaamilise tööviisi puhul muutub vedrukese võnkumise amplituud (ja faas) teraviku tipu ja objekti pinna vastastikmõju jõu gradiendi tõttu, mis on tingitud tipu ja pinna vahelise kauguse muutustest. Pinna topograafia signaal saadakse skanneri z-telje pinge muutusest (nagu C-AFM puhul), hoides tagasiside kaudu vedrukese võnkumise amplituudi (faasi) konstantsena.

Kontaktne:

skaneerib teravik objekti olles pehmes kontaktis objekti pinnaga. Teravikule mõjuvad jõud on tõukejõud, keskmise väärtusega 10 nN.

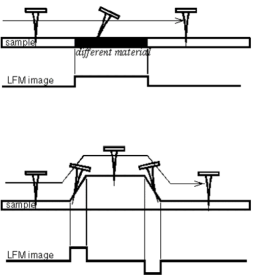
AFM kontakt-viisi korral võtavad tipupinna tõukelisest vastasmõjutusest osa kõik elektronid, mis on seotud tipu all asuvate objekti pinna aatomitega. Selle tõttu kirjeldab AFM kujutis pinna lokaalse olekutiheduse ρ(r, E) muutusi kogu energiaskaala ulatuses.

Peale vertikaalsete jõudude mõjub liikuvale teravikule ka lateraalne jõud, mis on seotud objekti hõõrdeomadustega.

Konsooli lateraalne kõrvalekalle, mis on tingitud pinna hõõrdumise muutusest (ülemine); tõusu muutusest (alumine).

Mida tuleb arvestada AFM rakendamisel objekti visualiseerimiseks vedelates keskkondades?

5. Kuidas muudetakse suurendust AFM puhul?

Millist informatsiooni on võimalik saada AFM piltidelt?

AFM kontaktviisi korral võtavad tipu-pinna tõukelisest vastasmõjutusest osa kõik elektronid, mis on seotud tipu all asuvate objekti pinna aatomitega. Selle tõttu kirjeldab AFM kujutis pinna lokaalse olekutiheduse ρ(r, E) muutusi kogu energiaskaala ulatuses - seega AFM kontaktviisi puhul on tegemist tõeliselt topograafilise pildiga, mis ei ole alati nii STM puhul.

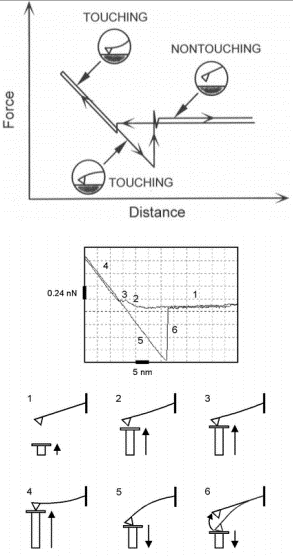
Skaneeriv jõu-spektroskoopia uurib lokaalselt F ~ d sõltuvusi. Neilt kõveratelt saab määrata adhesioonijõudu eri materjalide vahel, kasutades erinevast materjalist teravikke.

Varieerides iga pikseli puhul objekti kõrgust etteantud jõu ulatuses, saab visualiseerida pinna jäikuse/elastsuse lokaalseid erinevusi - jõu modulatsiooni meetod.

Peale vertikaalsete jõudude mõjub liikuvale teravikule ka lateraalne jõud, mis on seotud objekti pinna hõõrdeomadustega.

Selgitada hõõrdejõu mikroskoopia põhimõte

jõu-spektroskoopia põhimõte

Skaneeriv jõuspektroskoopia uurib lokaalselt F ~ d sõltuvusi. Neilt kõveratelt saab määrata adhesioonijõudu eri materjalide vahel.

Kuna konsooli deformatsioon on elastne, saab objektile mõjuva horisontaalse jõu F leida konsooli vertikaalse painde s abil vastavalt Hooke seadusele F=ks (k – vedrukonst) (vt. eest!)

Jõu suurus määratakse jõu diagrammilt, kus vahemik näitab skänneri pikkuse muutust (viimane on võrdne teraviku paindega s, kui kaugus on, d=0).

6. Milleks kasutatakse kalibreerimisobjekte teravikmikroskoopias?

7. Selgitada AFM-ga tehtava nanolitograafia põhimõtteid.

Probleemküsimused:

Saab uurida isolaatoreid

1. Miks teravikmikroskoop ei vaja läätsesid objekti kujutamiseks?

2. Valida sobivad töömeetodid järgmiste objektide uurimiseks ja põhjenda valikut:

• Kleepuva teibi pind – mittekontaktne tööviis

• Korrodeerunud metalli pind, mis on kohati kaetud koheva korrosiooni

• produktide kihiga

• Poleeritud terase pind

• DNA molekul

3. Mõningatel juhtudel kasutatakse AFM puhul juhtivast materjalist teravikku, milliseid lisavõimalusi see annab proovide uurimiseks? Selgitada ka milliseid AFM tööviise igal konkreetsel juhul kasutatakse.

4. Kas AFM abil on võimalik uurida auto värvipinda autot vigastamata?

Skaneeriv tunnelmikroskoopia

8. Selgitada tunnelefekti kvantolemust ja tuua tunnelvoolu sõltuvus rakendatud pingest ning tunnelvahemiku parameetritest.

Tunnelefekt

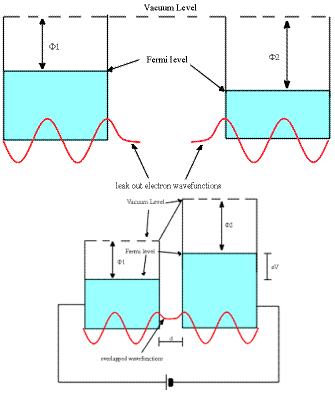
Tunnelvool tekib elektrit juhtiva pinna kohal hõljuva pingestatud teraviku ja pinna vahel, kui pinge, U, on väike ja vahemik teraviku ja objekti vahel, d, on võrreldav aatomtasandite vahelise kaugusega kristallis. Tegemist on kvantnähtusega: elektronid on suutelised läbima teatud kõrguse ja paksusega potentsiaali barjääri, kuna nad omavad laineomadusi. Tekkivat voolu nim. tunnelvooluks ja see avaldub väikeste pingete puhul:

Seos (1) kehtib väikeste pingete korral (kui ei esine väliemisiooni), siin

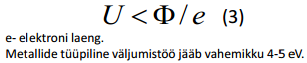
Selgitada mõistet skaneerimine ja mehaaniline skaneerimine.

Mis on STMil erinev; ei saa kasutada kiiret skaneerimist, peab reageerima objektile?

Selgitada skaneeriva tunnelmikroskoobi ja selles kasutatava toruskanneri tööpõhimõtet.

9. Selgitada mõisteid lokaalne bärjäärikõrgus ja

Valemist (1) nähtub, et tunnelvool sõltub nii tunnelvahemikust, kui lokaalsest barjääri kõrgusest. Seega STMpildi kontrast võib olla tingitud nii pinna korrugatsioonist (topograafia), kui ka barjääri muutusest pinnal, seega pinna omaduste muutusest (NB! ka teraviku pinna omadustest). Neid kahte efekti saab eraldada, diferentseerides seost (1) d suhtes konstantsel pingel:

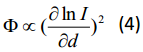
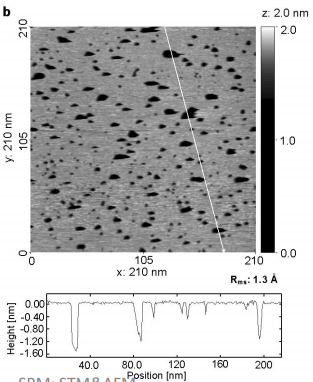
Eksperimendis pannakse teravik vibreerima ning mõõdetakse/mapitakse lokaalse barjääri muutuseid pinnal. Tegelikult sisaldab selline jaotuspilt teatud määral ka topograafilist informatsiooni ja seda on raske eristada väljumistöö muutustest. Seega tuleb sellistesse eksperimentidesse suhtuda erilise ettevaatusega.

Vedelas N2-s lõhestatud Bi (111) tahu UHV-STM topograafiline kujutis. Tumedad alad (väiksem tunnelvool) näivad aukudena, on aga tegelikult Bi-oksiidi saarekesed, s.t. kõrgendikud, kuid neil on elektronide väljumistöö tunduvalt suurem, kui puhtal metallil.

lokaalne olekutihedus ning selle jaotus, ja täidetud ning täitmata olekud - kasutades energiadiagramme.

Kuna tunnelvool sõltub elektronide lokaalsest olekutihedusest (kindla energiaga elektronide arv antud punktis, r), siis lokaalne tunneljuhtivus σ1/R=I_t/U avaldub:

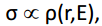
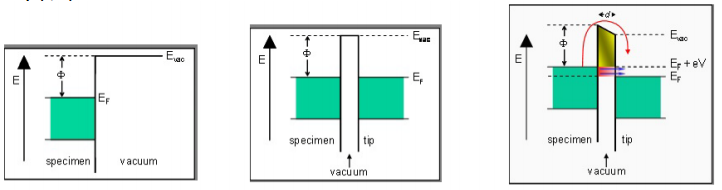kus ρ(r,E)- lokaalne olekutihedus.

LDOS jaotuse saamiseks mõõdetakse katsetes sageli suuruse (dI/dU)/(I/U) muutusi sõltuvalt U-st.

Hoides tunnelvahemiku konstantse ja mõõtes tunnelvoolu muutust sõltuvalt pinge muutusest saab määrata LDOS väärtust objekti punktis. Liikudes objektil ringi, saab kaardistada (mappida) vastavaid muutusi pinnal. Muutes pinge polaarsust saab sondeerida täidetud ja täitmata seisundeid pinnal. Selline eksperiment on üks tunnelspektroskoopia (STS) liik. Seda saab teha ka aatomtasandil, kui mikroskoop on mehaaniliselt piisavalt stabiilne ja elektroonsed mürad on väikesed.

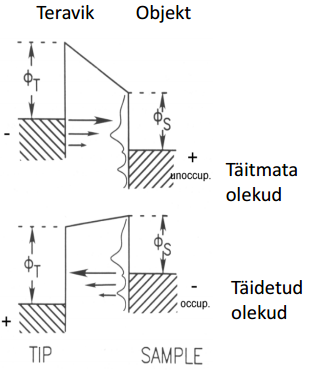Tsoonidiagramm objekti erineva polaarsusega pinge korral.

STM topogramm Si/(1/6MLAl). Ülal heledad Al adsorbeerunud aatomid (objekt +) ja all Si aatomid (objekt –).

Selgitada miks ja kuidas muutub STM piltide kontrasti polaarsus sõltuvalt rakendatud tunnelpinge polaarsusest.

Selgitada STM suurt ruumilist lahutusvõimet võimaldavaid printsiipe.

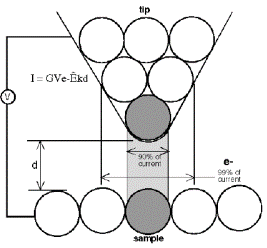STM puhul määrab potentsiaalselt suure (atomaarse) lahutusvõime tunnelvoolu eksponentsiaalne sõltuvus vahemikust teraviku tipu ja objekti pinna vahel:

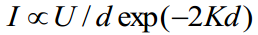
Reaalne (lateraalne) lahutusvõime sõltub suurel määral teraviku tipu kujust. Nii ei võimalda “nüri ja/või lame” tipp reaalset atomaarset lahutust.

Teraviku aatomite panus lahutusvõimesse: Tipuaatom 90%, II tase 9%; III tase 1%.

10. Milliseid tingimusi esitatakse objektidele nende uurimiseks STM meetodil.

Objekt peab olema juhtivast materjalist; objekti pind peaks olema küllaltki sile; puha, mustus pärsib tunnelvoolu.

Tuua näited STM rakenduste kohta.

Rakendused: pinna topograafia, aatomlahutus, adsorptsiooni, desorbtsiooni uuringud, keemilise oleku määramine.

Millised on põhilised eripärad STM-i rakendamisel in-situ elektrokeemilistes uuringutes?

Kirjeldada lühidalt teisi SPM perekonna mikroskoope.

Juhtivuslik AFM (cond-AFM)

Siin kasutatakse elektrit juhtivat teravikku-vedrukest ja tundlikku vooluvõimendajat.

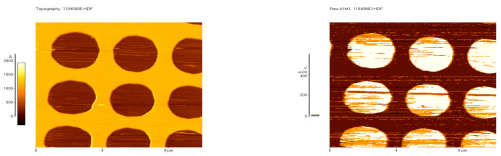
Vasakpoolsel pildil on testobjekti topograafiline kujutis ja parempoolsel samal ajal salvestatud juhtivuskujutis. Näeme, et reaalse pinna mustuse tõttu on fikseeritud voolujaotus väga ebaühtlane ka legeeritud ringikujulistel aladel.

Elektrokeemiline STM

ESTM eripära, et toimub sama-aegselt elektrokeemiline protsess. Lisaks 2 –le töö-elektroodile on veel abielektrood ja standardelektrood. Uurimisobjekt asub elektrolüüdilahuses. KOKKU 4 elektroodi.

Nt polümeerkilede kasvamine

Skaneeriv termiline mikroskoop

Termoteravik

Skaneeriv magnetmikroskoop (SMM)

Siin kasutatakse magneetilise kattega (Co, Ni) AFM teravikke ja mittekontakstset tööviisi.

Akustiline skaneeriv mikroskoop (ASM/SAM)

SiC fiibrid Al₂O₃ maatriksis - AFM kontakt-viisi kujutis (a) ja akustiline kujutis (b); 10x10 µm²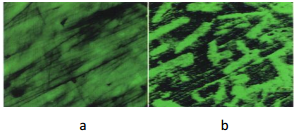

Optiline lähivälja mikroskoop (SNOM/NSOM)

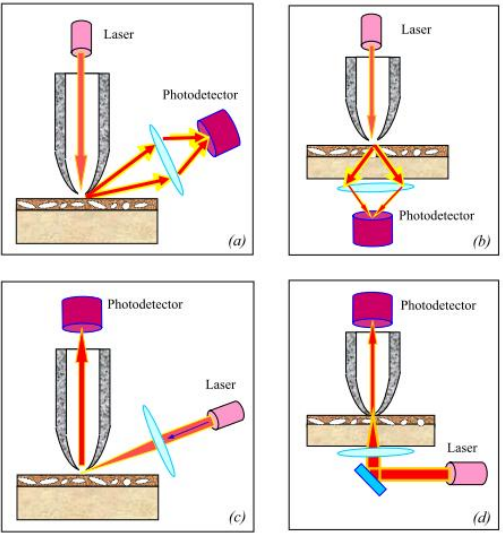a) Laserivalgus tuleb läbi fiibri ning peegeldub objekti pinnalt detektorisse;

b) Laserivalgus tuleb läbi fiibri ning läbib objekti (nn läbivkiirgus);

c) Laserivalgus peegeldub objekti pinnalt fiibrisse;

d) Laserivalgus tungib läbi objekt fiibrisse.

11. Võrrelda SEM ja STM – põhimõte ja olulisemad eelised ning puudused

Probleemküsimused:

1. Kumb lahutusvõime on STM-il reeglina suurem, kas lateraalne (ristisuunaline) või kõrgussuunaline lahutus, ja miks?

2. Miks on AFM-iga kergem uurida oksiidmaterjalide pinda, kui STMiga, ja miks?

3. Kas ja milliseid oksiidi pindu on võimalik uurida STM abil ja miks?

4. Selgitada, mis muutub, kui STM kambrist pumbata välja õhk / gaasid ja miks sageli kasutatakse aatomlahutuse saamiseks UHV tingimusi?

(Skaneeriv) läbiv elektronmikroskoopia - TEM

12. Võrdle TEM ja OM tööprintsiipi.

•Mõlemad mikroskoobid on projekteerivad ja alluvad laineoptika seaduspärasustele.

•OM lääts klaasist, TEM lääts elektromagnet, mille fookuskaugust saab muuta ergutusvooluga. NB! Elektronid ei kaota läätses kiirust ning liiguvad spiraalselt ümber optilise telje.

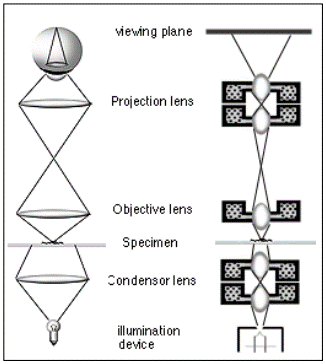•Kui OM-s kasutatakse Köhleri valgustussüsteemi, siis TEM puhul kasutatakse kriitilist valgustussüsteemi: kondensorlääts fokuseerib valgustusallika (Wennelti abil formeeritud hõõgniidi kujutise) objekti tasandile ligilähedaselt paralleelse kimbuna. Nii saavutatakse maksimaalne objekti valgustatus. Tavaliselt on elektronkiire läbimõõt objektil ~2 µm, mis on küllaldane, et täita suure suurenduse korral kujutisega kogu luminestseeruv ekraan. Kuna elektronmikroskoobi kondensorläätsed ei ole reeglina korrigeeritud, siis pole vajadust paigutada seda läätse mingi kindla fookuskauguse punkti. Seega saab elektronkimbu intensiivsust kontrollida/muuta kondensorläätse ergastuse abil, jättes valgusallika asukoha muutumatuks.

•OM puhul kasutatakse põhiliselt amplituudi-kontrasti. TEM puhul kasutatakse nii amplituudi- kui faasikontrasti.

•OM puhul muudetakse suurendust okulaari või objektiivläätse vahetamisega (uue läätsekomplekti ettekeeramisega). TEM puhul on objektiivläätse suurendus (fookuskaugus) fikseeritud, kujutise suurendust muudetakse projektsioonläätse fookuskauguse (ergastusvoolu) muutmisega.

•Elektronläätsedel esinevad tugevad aberratsioonid, kuna magnetvälja ei saa formeerida nii, nagu seda saab teha optilise läätse kujuga, seetõttu tuleb tugevasti piirata apertuurava, mis viib suurtele intensiivsuse ja lahutusvõime kadudele. Sellele vaatamata on elektronoptika lahutusvõime tuhandeid ja sügavusteravus sadu kordi parem kui OM-il.

•OM-il on väike fookuskaugus, s.t. objekti erinevaid tasandeid tuleb eraldi fokuseerida. TEM puhul seevastu on kogu (õhuke) objekt korraga fookuses. Uuritavad objektid peavad seetõttu olema väga õhukesed, tüüpiliselt on bio-objektid ≤ 100 nm, ja üleminekumetallide objektidel 10-50 nm paksused.

•TEM töötab vaakumis kuna elektronide hajumine isegi hõrendatud gaasides on väga suur.

Mille poolest erineb TEM ja STEM?

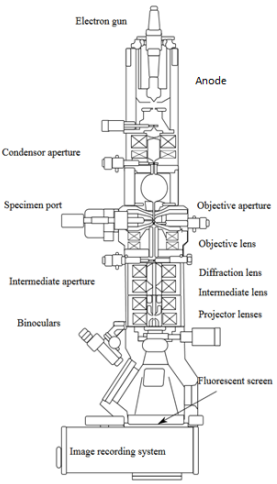Elektronide genereerimine elektronkahuris

Elektronide kiirendamine anoodi abil

Elektronkiirega manipuleerimine kondensorsüsteemis (magnetläätsed – kas STEMi või TEMi režiim. STEMi – fokusseeriv lääts, kiir tehakse kitsaks, skaneerimismähise abil liigutatakse kiirt, alumise mähisega tehakse kiirt kitsamaks, sellega skanneeritakse üle proovi objektil; TEMi – valgustatakse kogu ala)

Objektil kogu uuritava ala valgustamine (TEM) või skaneerimine fokusseeritud elektronkimbuga (STEM) – skaneerimismähiste abil.

Prooviobjekti liigutamine õige koha valikuks (objektihoidjat saab kuumutada/jahutada, liigutada asendisse, kuhu vaja)

Mitmete läätsede abil suurendamine (läätsede süsteem amplituudi või resolutsiooni režiim; määravad lisaks suurenduse; mida rohkem läätsi, seda parem suurendus)

Suurendatud kujutis fluorestsemtsekraanil (mõõtmise ajal näeb kujutist läbi pinokli)

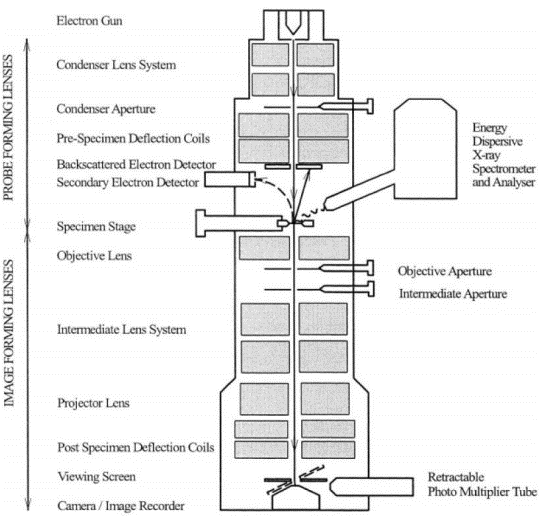
(S)TEM

üks võimsamaid materjalide mikro- ja nanoskaalas uurimise vahendeid

võimaldadab saavutada aatomlahutust

uurida õhukeste objektide struktuurseid omadusi

elementset ja keemilist koostist

ning teisi füüsikalis-keemilisi omadusi suure lokaalsusega

Kaasaegne seade on sageli

kõrg- (puhta) vaakumiga nii elektron-optilises kui ka uurimisobjekti kambris,

elektroonse kujutise registreerimisega

objekti 3D mani-puleerimisega (nihutamine, keeramine, kallutamine mitme telje ümber)

ning varustatud mitmekülgse analüütilise seadmestikuga

sageli saab objekti kuumutada kuni või üle 1000 K ja/või jahutada krüogeensetele temperatuuridele.

TEMis ei näe ühte aatomit, ühest vähe, peab terve kolonn aatomeid olema

TEMiga saab reaalajas nt ümberkristallumist vaadata

Objektid peavad olema niivõrd õhukesed, et sondi elektronid läbiksid objekti põhiliselt energiakadudeta,

keskmise aatomnumbriga objektid tüüpiliselt 10-50 nm, kui kasutatakse primaarelektronide energiat 80-400 keV.

Eriti suure läbitavuse ja sealjuures hea lahutusvõime saavutamiseks kasutatakse kuni 3 MeV mikroskoope, kuid siin peab alati hindama seadme maksumust, ekspluatatsioonikulusid ja võimalikku kasulikkust teatud probleemi(de) lahendamiseks.

TEM

Elektronide allikas

Asub mikroskoobi ülaosas

Sellest väljunud elektrone kiirendatakse pinge abil

Pinge valitakse vastavalt uuritava objekti materjalile, selle paksusele ja soovitavale informatsioonile

Madalama energiaga mikroskoopide lahutus paranenud => kõrge energiaga (kuni 3 MeV) mikroskoobid pigem haruldased

Tingitud parematest läätsesüsteemidest

Kvaliteetsemast proovi ettevalmistamisest

Olemas emissioonikahurid

Võimaldavad tekitada elektronkiirt, mille läbimõõt on 1 nm suurusjärgus

Kondensorsüsteem

Koosneb vähemalt 2 kondensorläätsest

Võimalik manipuleerida elektronkiirega

Muuta läbimõõtu, mis interakteerub prooviga

kui valgustame suuremat ala, siis intensiivsus, mis pinnale jõuab, on väiksem; kui valgustame väiksemat ala, siis intens, mis pinnale jõuab, on suurem.

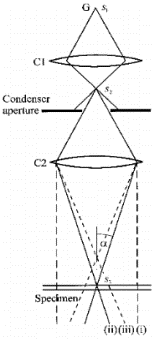kui paksemad materjalid, siis kiirt vaja rohkem kokku panna, et saada rohkem infot, muidu e^- ei jõua pinna sisse väga, siis aga see ala, mida näeme, väiksem

Kahe kondensorläätsega süsteem.

Kiire läbimõõt s1 muudetakse kondensorläätse C1 abil suuruseks s2.

Teine kondensorlääts on kasutusel kiire fokuseerimiseks.

Ta võib ka muuta kiirt suuruseks s3.

(i), (ii), (iii) näitavad seejuures alafokuseeritud, fokuseeritud ja ülefokuseeritud kiiri.

Koondumisnurka α saab muuta kondenserapertuuri abil.

Proovikamber

asub kondensorsüsteemi all

See on mikroskoobi kõige olulisem osa, kuna väga väikest prooviobjekti tuleb hoida väga täpselt õiges kohas

Seda teostatakse spetsiaalse hoidja abil

Samuti peab olema võimalik seda liigutada mitmeid millimeetreid ja kallutada suurte nurkade all

Kui on vajadus analüüsi järele, siis peab olema lubatud ka röntgenkiirguse pääsemine prooviobjektilt detektorisse

Mõnel juhul on vajalik ka objekti hoidmine väga madalatel või siis teinekord väga kõrgetel (kuni 1000 ⁰C). Ka selle jaoks on olemas spetsiaalsed hoidjad

Objektihoidjad

Ühe telje kallutusvõimalusega objektihoidja

Objekti vahetamine on lihtne ja kiire, kuna proov fikseeritakse ühe klambriga ja hoidja saab seadmesse paigaldada läbi lüüsisüsteemi, mis vajab vaid paar minuti pumpamise aega

On ka kuumutamist lubavadi objektihoidjaid

kuumutamine: kristallstruktuuri muutuste uurimine reaalajas (nt titaanoksiid); probleem: elektronkiire enda energia tõttu toimuvad ka krist.strukt muutused

Miks on suurte suurendustega mikroskoopide kasutamiseks vajalik kasutada kiirendatud elektrone?

Selgitada mõisteid amplituudi-, massi- ja difraktsioonikontrast TEM-is.

Amplituudi- ja difraktsioonirežiim

Amplituudi kontrasti režiimis moodustub kujutis

õhukest objekti pikihajumisega läbinud (väikeste nurkadega elastselt hajunud) elektronide abil (heleväli)

helevälja pilt: detekteeritakse neid elektrone, mille hajumisnurk on minimaalne (nt 1 kraad)

heleväljapildil raskemad elemendid tumedamad (elektronide hajumine ja elektron ei saa sealt otse nii kiirelt läbi minna)

või suuremate nurkade all elastselt hajunud elektronide abil (tumeväli).

Tumevälja režiim: detekteeritakse neid elektrone, mis hajuvad rohkem (nurk primaarkiire telje suhtes suurem), nende puhul saame hoopis teistsugust infot proovi kohta

Tumeväljapildd peaks tunduma heledamad

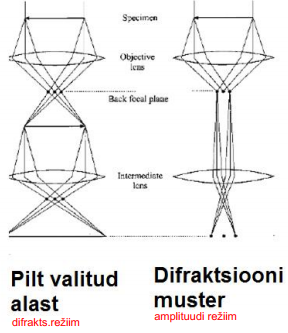
Heleväli vs tumeväli

Heleväli ja tumeväli on kõige laiemalt kasutatavad pildi saamise viisid

Helevälja (BF) korral

on objektiivläätse fokaaltasandi keskele asetatud väikese avaga apertuur, mis laseb läbi vaid hajumata elektronid ja blokeerib hajunud elektronid.

Tumevälja (DF) korral

on apertuur nihutatud optilisest teljest eemale, et blokeerida hajutamata kiirt ja registreerida vaid hajunud kiirt.

Vastavalt sellele on ka saadud kujutised erinevad.

Nimelt hajutavad elektrone rohkem kõrgema aatomnumbriga või paksemad kohad. Seega on ta ka BF pildil tumedam ja DF pildil heledam.

Kristalliliste objektide korral on hajumise intensiivsus jällegi suurem kindlates suundades, mille tulemusena saadakse tugev kontrast aladest, kus toimub valitud suunaline difraktsioon.

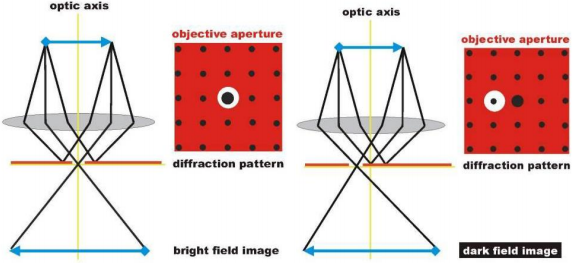
Massipaksuse kontrast

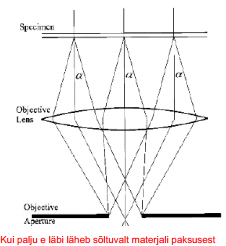Kui elektroni hajumisnurk on suurem kui 1 , siis ta ei lähe läbi ava (reeglina 20, 50 või 100 µm) ja seega ei osale ka pildi genereerimises.

Sageli peab α olema alla ühe kraadi

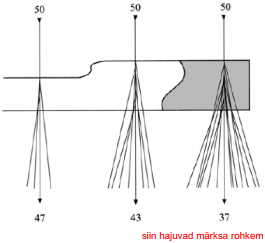Elektronide hajumine erinevates proovi osades. Vasakul, õhemas alas läbib 47 elektroni 50-st esialgsest.

Keskel, sama tihedusega aga paksemast materjalist läbib 43 elektroni 50-st esialgsest.

Paremal, tihedamast materjalist läbib vaid 37 elektroni.

Massipaksuse kontrasti näide

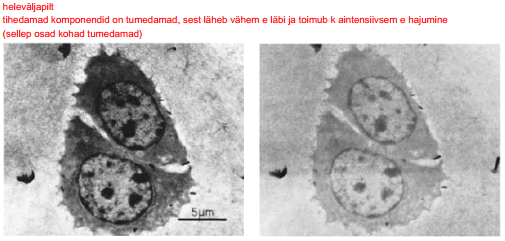
13. Selgitada faasikontrasti mehhanismi TEM-is.

Üks kõige tavalisem ja kasulikum on faasikontrasti pilt, mis saadakse nii et primaarkiir on täpselt paralleelne kristalli aatomtasandiga. Seega saadakse heledatest ja tumedatest punktidest koosnev pilt, kus igale punktile vastab mingi aatomite kolonn. Samas ei ole piltide interpreteerimine lihtne sest kontrast sõltub oluliselt proovi paksusest, fokuseerimisest ja lahutusvõimest. Näiteks võib sama mikroskoobiga tehtud pildil vastata tumedale täpile aatomite kolonn, nende vaheline tühi ala või isegi kahe aatomi kolonn.

Loengus kirjutatud: kristalliliste mat uurimine: proovi ettevalmistus nii, et kiired oleks suht paralleelsed nende tasanditega nt grafeen mingi kindla aluse peal (1 aatomikiht), uurimine: risti pinnaga pole läbi mõtet vaadata, sest on vaja aatomite rida, sellep tuleb vaadata küljelt tuleva kiirega; kui siledad nm-sed kihid, siis saab juba suht ilusa pildi (st pole 1 aatomkiht, vaid ikka rohkem)

Mille poolest erinevad, sarnanevad SEM ja STEM analüütilised võimalused?

Kumb kõrglahutusega mikroskoopidest SEM või (S)TEM võimaldab kristallilise objekti aatomlahutust ja miks?

(S)TEM

14. Energiakadude spektromeetria

15. TEM objektide valmistamise viisid

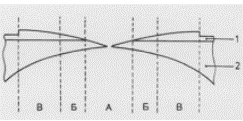“Ajalooline” TEM objektide prepareerimine: lõikamise, õhukeseks lihvimise ja keemilise ning ioonsöövitamisega viimistlemine.

Kaasaegne lokaalne (S)TEM objekti prepareerimine: FIB söövitamine, lamelli lahtilõikamine ja manipulaatoriga spetsiaalse objektihoidja juurde viimine ning külge kinnitamine.

Mikrotoom

Terava lõiketera abil lõigatakse õhukesed viilud uuritavast materjalist, mis asetatakse TEM objektihoidja võre peale.

Viilud peavad olema seejuures piisavalt õhukesed, et teatud energiaga elektronid suudaksid seda läbida – alla 100 nm kergemate elementide korral.

Näiteks võib nanopulbrit segada polümeerse maatriksi sisse ja seejärel saadud nanokomposiitsest „vorstist“ parajad viilud lõigata, et TEM-is nende osakeste suurust määrata.

16. Kuidas tekib STEM-s Z-kontrast?

Mitteelastne hajumine on proportsionaalne aatomi numbri ruuduga. Kõrgema aatominumbriga element on seega tumevälja pildil heledam ja see võimaldab saada täiendavat informatsiooni keeruliste materjalide kohta.

Tugevasti difrageerunud elektronid, HAAD.

Probleemküsimused:

1. Katseobjektiks on mitmekihiline grafeen Si alusel. Eesmärk on võimalikult täpselt ära määrata TEMi abil kihtide arv.

• Kirjeldada proovi ettevalmistust ja asetust elektronkiire suhtes

• Valida sobiv elektrone kiirendav pinge ning põhjendada

• Mida tuleb arvesse võtta grafeeni kihtide määramisel st TEM pildi

• interpreteerimisel?

2. Katseobjektiks on W-Al sulam, milles esinevad väiksemad ~10 nm suurused metallifaasid. Vaja on teha kindlaks nende faaside täpne suurus ja uurida kas nad on kristallilised või amorfsed.

• Kirjelda proovi ettevalmistust

• Valida sobiv kiirendav pinge

• Mille järgi interpreteerida TEM pilti?

3. Kuidas määrata TEMi abil Au nano-osakeste täpne suurus?

• Kirjelda proovi ettevalmistust

• Kuidas valida sobiv kiirendav pinge

• Mille järgi interpreteerida TEM pilti?

Fotoelektron- ja Auger elektron spektroskoopia

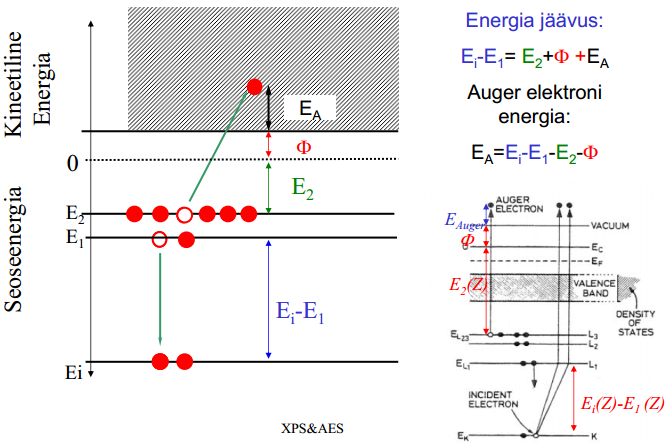
17. Selgitada fotoelektrilist efekti elektronide energiadiagrammi abil, võrdle seda röntgenkvandi ja Auger elektroni genereerimisega – tuua lisaks ka selgitavad skeemid.

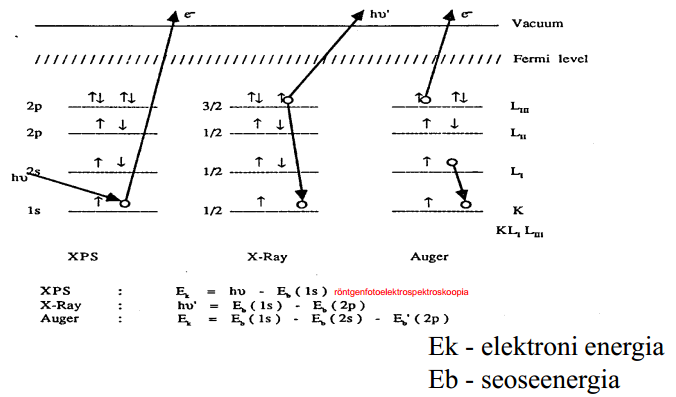
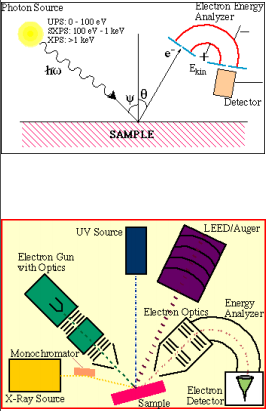
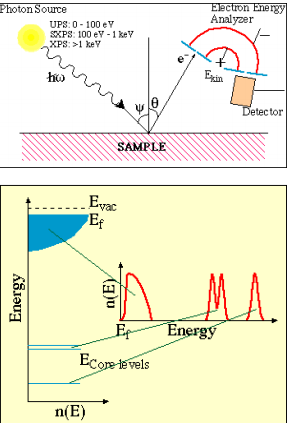Fotoelektronide (FE) genereerimiseks kiiritatakse ülikõrgvaakumis asuvat objekti (monokromaatse) elektromagnetilise kiirgusega, footoni energiaga hυ=ħω, mille neeldumise tagajärjel ioniseeritakse erinevatel energianivoodel asuvaid elektrone, s.t. genereeritakse fotoelektrone, mis objekti pinnalähedasest ruumist on võimelised objektist väljuma (fotoelektriline efekt). Sealjuures tahkisest lahkuvate elektronide kineetiline energia avaldub:

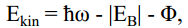
kus E_B- on elektroni seoseenergia ja Φ- on elektroni väljumistöö antud ainest – viimane liige on atomaarsete gaaside korral null! Väljuva elektroni moment p (vektor!) on määratud kineetilise energia abil:

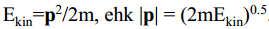
Momentvektori p suuna määravad asimuutnurk θ ja polaarnurk φ, mille suunas elektron lahkub ainest. Teades footoni energiat ja väljumistööd, saab mõõdetud kineetilise energia abil määrata elektronide seoseenergia E_B. Seega näitab fotoelektronide spekter kujukalt aine aatomite elekt ronkatete energeetilist struktuuri (aatom- või molekulaarorbitaalid, või valentstsoon, vastavalt atomaarses või molekulaarses gaasis, või tahkises), ning see saadakse paljude fotoelektronide energia määramisel (elektrostaatilise) elektronspektromeetri abil.

Fotoelektriline efekti avastati eeldades, et aatomites neeldub kiirgus diskreetsete energiaportsjonitena, E=ħω, ja see energiamuutus on seotud massi ning impulsi muutustega, vastavalt E=mc₂ ning p=mc=hν/c=ħω/c (nn. Einsteini seosed).

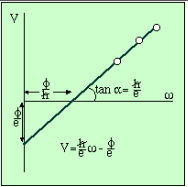
Maksimaalne fotoelektronide kineetiline energia E_max,kin määrati minimaalse välise pinge V_R abil, mis katkestas fotoelektronide voo metallist vaakumanumale. Muutes ergastuse energiat (e. lainepikkust), määrati Plancki konstandi suhe elementaarlaengusse, ħ/e, ja elektronide väljumistöö, Φ:

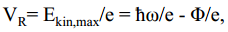
sest maksimaalse kineetilise energiaga lahkuvad metallist nn. vabad elektronid, mille E_B=0. Seosed V ~ ω on erinevate materjalide puhul sirged, mille tõus on määratud fundamentaalse suuruse ħ/e-ga (seega kõigile ainetele ühesugune), ning mis on üksteisega nihkes Φ/ħ võrra, s.t. väljumistööde erinevuse tõttu eri ainete puhul (vt. skeeme ülal)

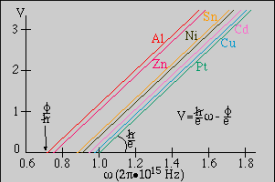
XPS - X-Ray Photoelectron Spectroscopy – röntgenfotoelektronspektroskoopia;

PES - Photoelectron Spectroscopy – fotoelektronspektroskoopia;

UPS - Ultraviolet Photoelectron Spectroscopy – ultraviolett fotoelektronspektroskoopia.

ESCA - Electron Spectroscopy for Chemical Analysis – elektronide spektroskoopia keemilise analüüsi jaoks (siia alla võib kuuluda ka Auger elektronide spektroskoopia)

Defineerida elektroni väljumistöö tahkisest.

Elektroni väljumistöö on minimaalne energia, mis peab olema antud elektronile, et lüüa see välja uuritava aine pinnast. Fotoelektrilise efekti korral saavutatakse elektroni ergastus footoni absorptsiooni läbi. Kui footoni energia on suurem kui uuritava aine elektroni väljumistöö, siis toimub fotoelektriline emissioon. Φ=h*f₀

H – Planki konstant, f₀ – minimaalne vajalik footoni sagedus tekitamaks fotoelektrilist emissiooni.

Defineerida elektronide vabalennu teepikkus, ja mida see iseloomustab?

Mitteelestne elektronide vabatee pikkus (pikkus kahe mitteelastse põrke vahel), määrab energiakadudeta liikunud elektronide väljumissügavuse. Mitteelastne elektronide vabatee pikkuse sõltuvalt nende kineetilisest energiast määrab seega

informatsiooni sügavuse pinnaanalüüsil

nõuded pinna puhtusele ja vaakumi taseme analüüsil.

määrab vaakumi taseme analüüsil: p=10^-4 torri puhul kattub pind monokihiga 1 s jooksul; p=10^-10 torri puhul kattub pind monokihiga 2h jooksul.

Mitteelastne elektronide vabatee pikkus sõltub nende kineetilisest energiast.

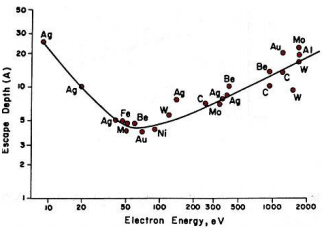Mingil emissiooni sügavusel d on võimalik arvutada tõenäosus, et emiteerunud elektron jõuab pinnale. Mida suurem d väärtus, seda väiksem tõenäosus P. Vähenemine toimub eksponentsiaalselt vastavalt P(d)=e^(-d/λ)

XPS ja AES spektrite backround noise on tingitud elektronide mitte-elastsest shokist, piigid aga elektronidest, mis jõudsid pinnale mitte-elastsete interaktsioonideta.

Mitte-elastne shok ja seega backround noise’i rohkus spketris on seotud kihi paksusega, mille elektronid peavad läbima:

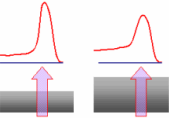
18. Milliseid ergastusi kasutatakse (foto)elektronspektromeetrias, ja milliseid erinevaid võimalusi need pakuvad?

Kaasajal kasutatakse elektronspektroskoopias ergastamiseks, s.t. objekti (gaas või tahkise pind) aatomite või molekulide ioniseerimiseks

ultraviolett-,

röntgen- või

sünkrotronkiirgust,

vastavalt UV -lambi, röntgentoru või sünkrotronallika abil. Selle tagajärel emiteeruvad objektist

foto-,

Auger- ja

sekundaarelektronid,

mida analüüsitakse elektronspekromeetri abil.

Kui ergastuskiirgus on polariseeritud (näit. sünkrotronkiirgus), võib lisaks elektronide kineetilisele energiale E_kin analüüsida ka nende impulssi p, milleks on vajalik kasutada nurklahutusega elektronspektromeetreid. Viimasel juhul määratakse fotoelektronide väljumisnurkade, θ ja φ, jaotusfunktsioon sõltuvalt pealelangeva kiirguse nurgast, ψ (vt. skeem vasakul ülal).

Teades ergastuse kvandi energiat ja elektronide väljumistööd objektist saab määrata elektronide seoseenergia, E_B, objektis:

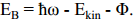
Kõrvalolev skeem näitab tüüpilist mitmefunktsionaalset pinnauurimise katseseadet.

Röntgenergastus: monokromaatse ergastuse eelised/puudused:

Eelised:

paraneb spektraalne lahutusvõime (Al Kαjoone laius on monokromaatoriga 0,5 eV ja monokromaatorita 0,85 eV;

puuduvad intensiivsete röntgenjoonte satelliitjooned;

Väheneb märgatavalt fooni tase.

Puudused:

Vähendab kiirguse intensiivsus;

Ergastusallikas on kallis ja vaja suuremat montaažiruumi.

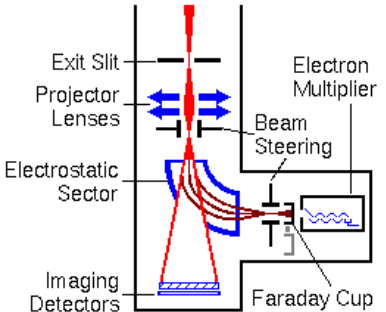
Selgitada poolsfäärilise (hemisfäärilise) elektronspektromeetri ehitust vastava skeemi abil.

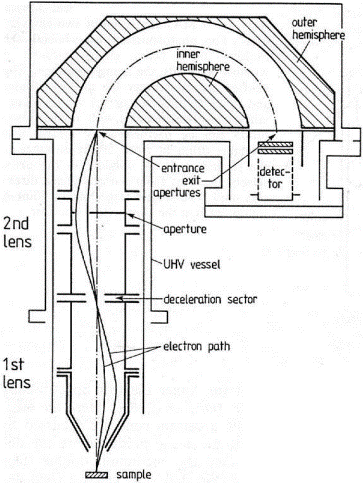Poolsfääriline elektronide spektromeeter-analüsaator koosneb kahest sisendläätsest, mis fokuseerivad sisenevad elektronid spektromeetri sisendavale, kust need satuvad poolsfäärilistele elektroodidele ja detektorisse. Selline elektronoptika võimaldab koguda emiteeruvaid elektrone piiratud pinnaalast, kuigi ergastusala võib olla lai.

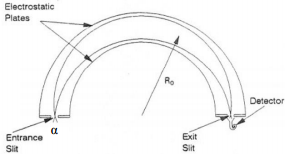
Spektraalse lahutusvõime suurendamiseks tuleb vähendada sisendnurka ja/või sisendpilu laiust, mis mõlemad kahandavad signaali tugevust – tuleb leida kompromiss.

Detektorina kasutatakse sageli sekundaarelektrone kordistavaid seadmeid, kas ühekanalilisi või uuemates seadmetes multikanalplaate. Signaali võimendamine põhineb siin sekundaarelektronide laviini tekitamises (sek. el. saagis > 1). Kõige efektiivsemad detektorid on CCD kaamerad.

19. Selgitada mõistet keemiline nihe.

Keemiline nihe on aine keemilise oleku/struktuuri muutumisest tingitud erinevus sidemeenergiates. Nihe aatomite sisekihi elektronide energias spetsiifilise aatomiümbruse muutuse tõttu. Fotoelektronjoonte nihe nt. aine eri kihtide aatomite erinevast ümbrusest tingituna.

Spektris keemiliste nihete jälgimine kihi kasvades.

Keemiline nihe:

Erinevates keemilistes olekutest parinevate fotoelektronide seoseenergiad erinevad

Seda pohjustab:

laengute jaotuse erinevus erinevates keemilistes olekutes

erinev laengute relaksatsioon sisekihi augu umbruses.

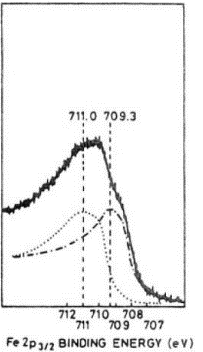Fe (709 eV) pinnal oksiidi Fe₂O₃moodustumisel nihkub 2 p_3/2 piik suuremate seoseenergiate poole (711 eV).

Kuidas toimub elementide profiilide määramine elektronspektromeetria abil?

Millel põhineb fotoelektron-ja Auger elektronmikroskoopia, võrdle seda SEM-iga.

Auger elektronide spektroskoopia

Röntgenkiirguse emisiooni iseloomustab fluorestsentsi saagis ω. Konkureeriva Auger-protsessi tõenäosus (Auger-elektronide saagis) avaldub röntgenkiirguse fluorestsentsi saagise kaudu:

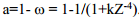
Näeme, et Auger-protsess on tõenäolisem kergetes elementides.

AES kasutab tavaliselt ergastamiseks elektrone

Auger protsessi seisukohalt ei ole olulist vahet, kas auk tekitada footonite, elektronidega või muude osakestega

Mõningased erinevused võivad siiski erinevate ergastuste korral tekkida, kuna

ergastavate kiirguste ja osakeste sisenemissügavused erinevad

mitmekordse ioniseerimise tõenäosused erinevad

Auger elektronide tähistamine

Üleminek ABC tähendab, et auk kihis A täidetakse elektroni poolt kihis B ning aatomist viiakse välja veel üks elektron kihist C;

KLL tähendab üleminekut, kus algseisundis on auk K kihis ja lõppseisundis 2 auku L kihis;

LMN tähendab üleminekut, kus algseisundis on auk L kihis ja lõppseisundis augud M ja N kihtides;

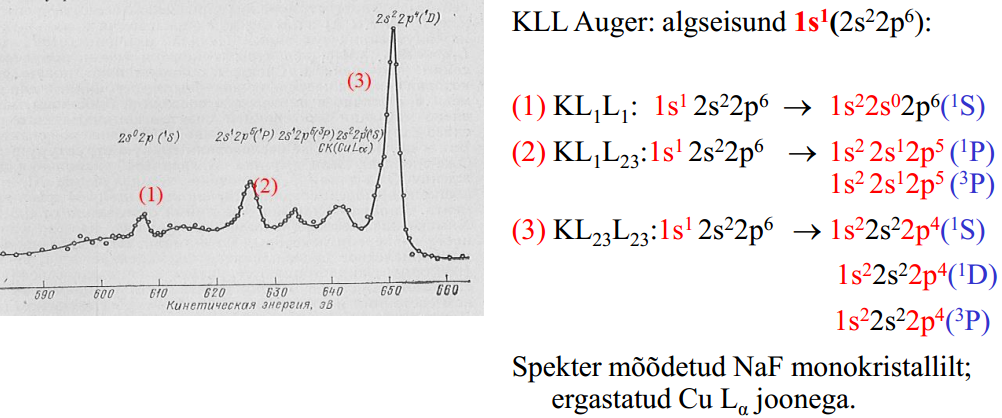
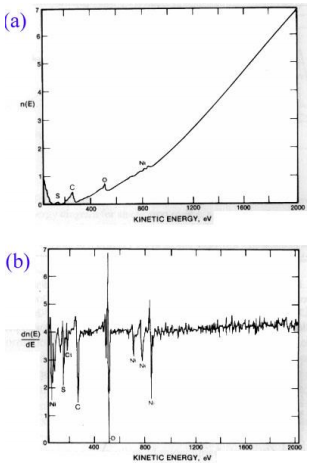Integraalne ja diferentsiaalne Auger-spekter

Kõrval on toodud saastatud pinnaga Ni-objekti Auger-spektrid, (a)- integraalne ja (b)- diferentsiaalne. Suurem osa Auger-analüsaatorites töötab diferentsiaalrežiimis, mis on tunduvalt tundlikum, tänu signaal-müra suhte paranemisele signaali diferentseerimisel.

Diferentsiaalse spektri puhul loetakse kokkuleppeliselt Auger-joone asukohaks diferentsiaali alumise piigi asukoht, seetõttu need jooned ei lange täpselt ühte integraalsete piikide asukohtadega.

Informatsiooni sügavus elektronergastusega pinna-anaüüsil

Varieerides uuritavate Auger elektronide energiat, saab varieerida uuritava kihi sügavust 10 nm piires (NB! siin energia varieerimine tähendab Auger-joone valimist – selle energia ei sõltu elektronide primaarenergiast).

Kiht-kihiline analüüs

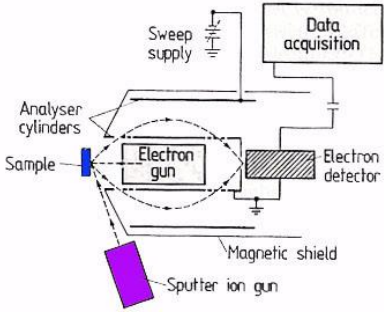
Kompaktne Auger-analüsaator koos ioonpihustamise kahuriga. Primaarelektronide kahur asub silinderanalüsaatori keskel. Kui seadmele lisada elektronkiire skaneerimispoolid, saab uurida elementide jaotust pinnal – Auger mikroskoop. Kui varustada ioonkahur skaneerimispoolidega, on võimalik pihustada suurema pindalaga nelinurkset kraatrit, mis koos ioonkimbu langemisnurga vähendamisega tasandan kraatri põhja pinna. Samuti tuleb kasutada võimalikult madalaenergeetilisi primaarioone, tavaliselt E₀ < 1-3 keV. Nimetatud meetmed tagavad objekti aatomite väiksema segregatsiooni (segipaiskamise) pihustustsoonis.

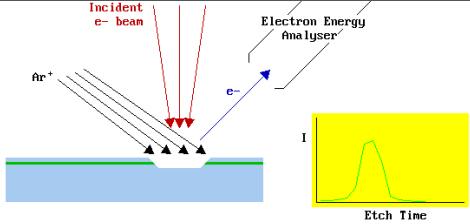
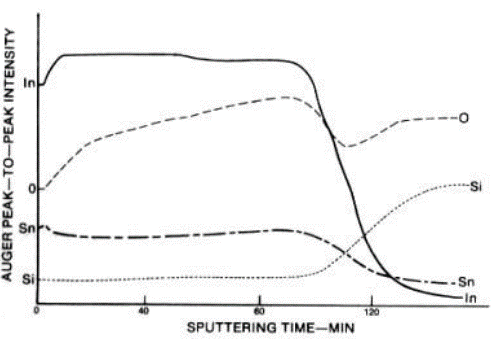InSnO kile Si-alusel, elementide profiilid, mis on saadud Auger-analüüsiga ioonpihustamist kasutades.

Kordamisküsimusi

Fotoelektroni, Auger elektroni ja karakteristliku röntgenkiirguse teke + energiate valemid ning kuidas on sellest kasu materjali karakteriseerimisel

Fotoelektronspektroskoobi ja Auger elektron spektroskoobi põhimõtteline plokkskeem

Kuidas on teostatud fotoelektronmikroskoopia? + näide

Kuidas on teostatud Auger elektron mikroskoopia? + näide

Õhukese kihilise materjali uurimine ioonpihustamise ja AES-iga

Fotoelektronspektroskoopia – keemilise oleku (näiteks oksiidi) tuvastamine – kuidas muutub seoseenergia

Fotoelektronmikroskoopia – erinevate keemiliste olekute jaotuse uurimine katseobjekti pinnal

Lühendid: XPS, PES, UPS, ESCA, AES, AEM

Auger elektronide tähistamine ja kirjeldamine või põhjendamine miks üleminek ei toimu; KLL, MKL, LMN, LMM, LNM

Probleemküsimused:

1) Miks saab Auger-elektronide abil kaldlihvi peal määrata elementprofiili objekti pihustamata?) Kui on vaja määrata pinnale segregeerunud üleminekumetalli õhukese kihi (võib olla saareline) pinnajaotust, millise meetodi valiksite (põhjenda)? Selgitada kuidas saab foto- ja Augerelektronmikroskoopiate abil uurida metallide lokaalset oksüdeerumist.

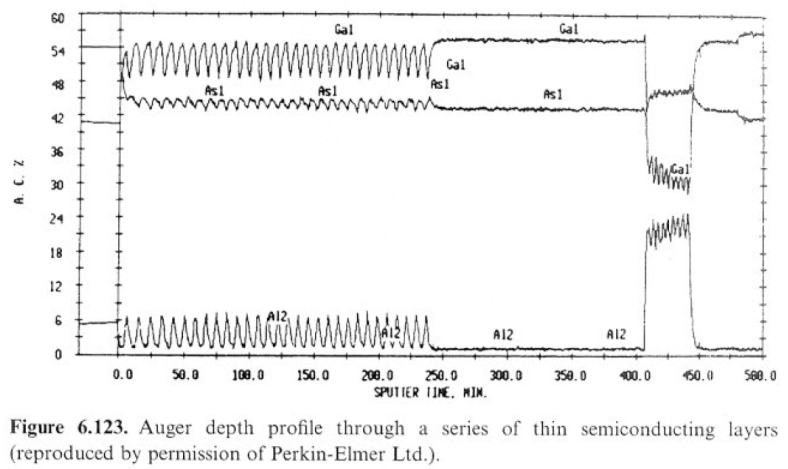
2) Millist informatsiooni saab välja lugeda allolevalt jooniselt uuritava AlGaAspooljuhtstruktuuri kohta? Kuidas on mõõtmine teostatud? Mida näitab pihustamise aeg (sputter time)? Sekundaaarioonide mass-spektromeetria ja Rutherfordi tagasihajunud ioonide spektromeetria

Lennuaja mass-spektromeetria. SIMS mikroskoopia.

Sekundaarioonide massispektromeetria (secondary ion mass spectrometry, SIMS) puhul pommitatakse objekti pinda primaarioonide kimbuga (sondiga), objektist eraldunud sekundaarseid ioone analüüsitakse mass-spektromeetriga (MS).

SIMS on võimeline mõõtma kõiki perioodilisuse tabeli elemente ning andma nende isotoopilise jaotuse.

Kuna primaarioonid pihustavad objekti pinda, saab SIMS abil määrata elementide profiile, s.t. jaotust objekti pinnalt sügavusse.

Kui primaarioonide sond on väikese läbimõõduga, saab SIMS abil määrata objektis leiduvate elementide lateraalset jaotust pinnalähedases kihis.

Tänapäeval kasutavad SIMS seadmeid elektroonikatööstus, geoloogia, bio- ja materjaliteadlased.

20. Kirjeldada pihustusprotsessi, mida kutsub esile tahlisobjekti pinna pommitamine kiirendatud ioonide kimbuga: pihustamisprotsessi produktid; profileerimine.

Kiirendatud primaarioonide (Ar+, Ga+, O2+, SFm+, ioniseeritud fullereenid, jt.) kimp/sond läbimõõduga mõnest mikronist kuni ~50 nm) pihustab objekti pinna aatomeid/molekule, tekitades nii

ioone,

ioniseeritud molekule/radikaale,

elektrone ja ka

neutraalseid osakesi.

Kui ioonide energia on mõõdukas, E0 < 3keV ja primaarkimbu intensiivsus on väike, toimub pinna-aatomite pihustamine väga aeglaselt (nn. staatiline SIMS), millega on võimalik saavutada submonokihilist sügavuse lahutusvõimet.

Tavaliselt töötatakse siiski dünaamilise SIMSi piirkonnas (E0~5-30 keV), kus pihustamine on märksa intensiivsem ja ka juhitavam, mis tagab meetodi parema kvantitatiivsuse.

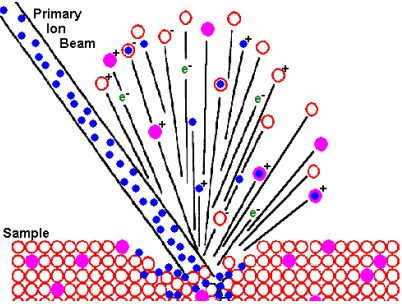
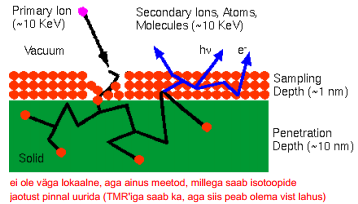Primaarioonide interaktsiooni objekti aatomitega seletab hästi nn. kaskaadmudel, eriti dünaamilises režiimis.

mudeli järgi annab kiire primaarioon oma energia objekti aatomitele järjestikustes binaarsetes põrgetes.

Lisaenergia saanud objekti aatomid põrkuvad uute objekti aatomitega, tekitades laviini.

Objekti aatomid, mis naaberaatomitelt tagasi põrkudes läbivad objekti pinna, st. väljuvad objektist, moodustavadki pihustunud materjali.

Pihustamine teeb objekti pinna karedaks ja võib põhjustada aatomite/molekulide segregatsiooni, kuna pealispinna aatomid võidakse lüüa kuni 10 nm kaugusele (NB! See on mitukümmend aatomkihti kristallis).

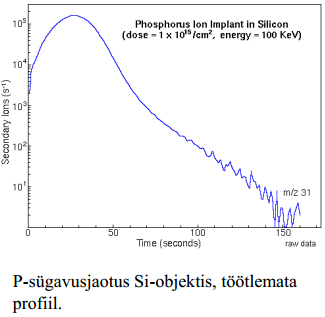Pihustamine/profileerimine

Pihustamise efektiivsus sõltub tugevasti primaar-ioonide omadustest: nii tekitab hapnikuioonide kimp rohkesti positiivseid ja metalli (Cs+, Ga+) ioonide kimp negatiivseid sekundaarioone. Samuti sõltub pihustamine objekti kristallstruktuurist, defektsusest, pingetest jt. mehaanilistest ning keemilistest omadustest. Et saavutada head sügavus-lahutusvõimet, pannakse primaarkimp skaneerima, nii et tekib suhteliselt lai lameda ja tasase põhjaga kraater. Seejuures kimbu jõudmisel kraatri servani, lülitatakse detektorsüsteem välja. Pihustamine toimub pidevalt ja häälestades massispektromeetri mingile kindlale ainele, saab määrata selle aine sügavusjaotuse.

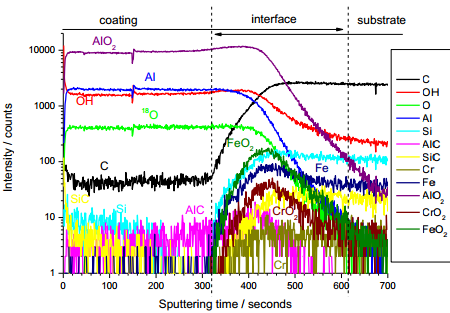Profileerimise näide: Al₂O₃/teras

lateraalne- ja sügavus-lahutusvõime;

Mass-spektromeetria põhimõte ja terminid: massi ja laengu suhe, massilahutus, mass-interferents, massidefekt, tundlikkus ja dekteerimise lävi.

Massispekter annab ioonide mass/laeng jaotuse. Selle saamiseks skaneeritakse massispektromeetrit teatud mass/laeng vahemikus sammuga, mis tagaks nõutud massilahutuse spektris. Massispekter näitab nii atomaarseid, kui molekulaarseid ioone, e. radikaale (rohkem, kui 1 aatom) ning ühe- ja mitmekordselt ioniseeritud osakesi. NB! Massispektromeetrias mõõdetakse massi ja laengu suhet: M/z. Samuti tuleb arvestada aatomite isotoopidega.

Massilahutus on, R=M/ΔM, kus M märgib lahutatud masse ja ΔM märgib lahutatud masside erinevust massiühikutes daltonites (1/12 ¹²C massist = 1.66054 × 10^-27 kg).

Massi-interferentsiga on tegemist, kui massispektris analüüsitava iooni mass langeb kokku (on liiga lähedal) mingi teise iooni massiga. Sellist interferentsi nimetatakse isobaariliseks. Nt ⁵⁶Fe⁺ analüüsimisel ränis, segab raua massijoont räni joon (²⁸Si₂)⁺, mõlema puhul on M/z≈56. Sageli põhjustavad interferentsi oksiidid, kuna Me-O side on suhteliselt stabiilne, seega võib raua (⁵⁶Fe⁺ ) signaali segada ka ioon (⁴⁰Ca¹⁶O)⁺.

Mõningatel juhtudel on võimalik kasutada analüüsiks sama elemendi mõnda teist isotoopi, nt ⁵⁶Fe asemel ⁵⁴Fe, mille mass erineb tunduvalt ²⁸Si₂ massist ning võtta arvesse isotoopide looduslikku vahekorda. Samas tuleb olla ettevaatlik, kuna mõned protsessid, nt ioonlegeerimine, võivad muuta looduslikku isotoopide jaotust.

Isobaarilisi masse aitab eristada massidefektiga määratud väga väikesed massierinevused nominaalsetes (prootonite ja neutronitega määratud) massidest. NB! Siit nõue suure massilahutusvõimega spektromeetritele.

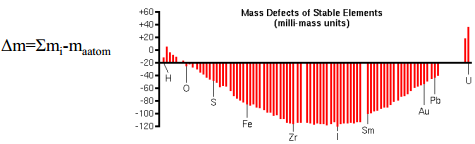
Tundlikkus ja detekteerimise lävi

Enamiku lisandelementide jaoks on SIMS detekteerimislävi 1012ja 1016aatom/cm3 vahel. Peale ioniseerimise efektiivsuse (RSF) võivad meetodi tundlikkust mõjutada ka teised faktorid. Üks tähtsamaid on detektori (fotoelektronkordisti, kanalplaat, CCD-kaamera) pimevool. See piirab tundlikkust, kui kasulik ioonsignaal jääb allapoole detektori pimevoolu taset. Teiseks, kui SIMS- seade ise genereerib analüüsitavat signaali, nt. hapnik või süsinik jääkgaasides, siis selline “müratase” piirab seadme tundlikkuse. Ka mass-interferents põhjustab foonist tingitud tundlikkuse languse, kuna tuleb töötada suurtel massilahustustel, seega vähendada spektromeetri väljundpilusid – sellega väheneb signaal/müra suhe. Samuti võib põhjustada tundlikkuse langust ioonkimbu skaneerimine ja profiili mõõtmise režiim.

SIMS seadmed, nende tööpõhimõte ja plokk-skeemid; staatilised ja dünaamilised mass-analüsaatorid.

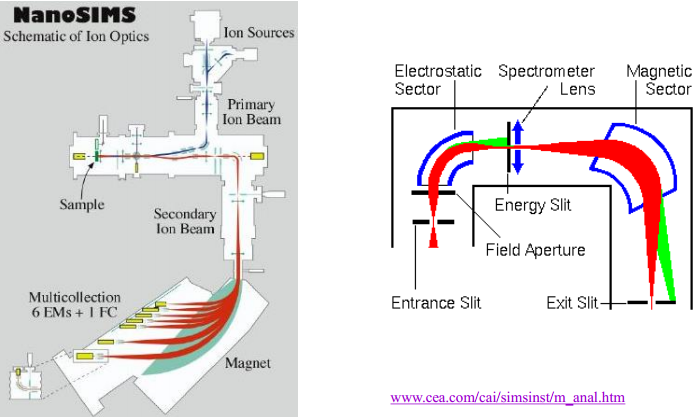Ioonide allikas, fokuseerimine, painutamine, uuesti fokuseerimine.

SIMS seadmed: kvadrupool-spektromeeter

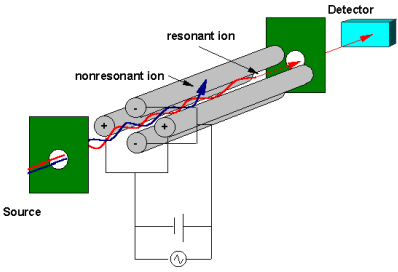Kvadrupool/spektromeetrid on väiksemad, kui magnetsektor spektromeetrid ja neid kasutatakse eriti seal, kus on vajalik ruumi kokku hoida, kuid saavutada suhteliselt head massilahutusvõimet, R<10000.

Süsteemis on kaks paari vardaid, mis on pingestatud. Seejuures on pingel alalispinge ja ka vahelduvpinge komponendid. See võimaldab vaid kindla massi / laengu suhtega ioonidel süsteemist läbi minna. Näiteks põrkuvad suurema laengu või väiksema massiga ioonid vardaga suurema tõenäosusega. Samas suurema massi ja väiksema laenguga ioone vahelduvpinge eriti ei mõjuta ja neid juhib pigem alalispinge.

Ioonlõksud: staatiline-ja dünaamiline massanalüsaator

Nii staatiline , kui dünaamiline analüsaator lõksustab analüüsitavad ioonid ja võimaldab neid seal lõksus manipuleerida.

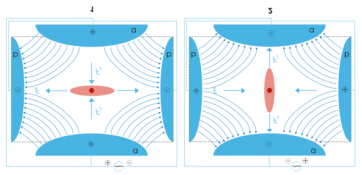
Staatiline analüsaator kasutab ioonide lõksustamiseks ja sorteerimiseks kuubikujulist ioonlõksu, mis töötab tsüklotron-resonantsi režiimis. Ioonid liiguvad magnetväljas ringikujuliselt kindla sagedusega. Kui energiat juurde anda siis raadius suureneb ja osake põrku vastu seina.

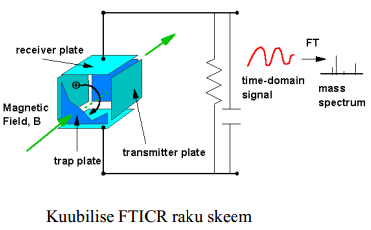
Dünaamiline analüsaatori puhul salvesta-takse ioonid 3D kvadrupoolsesse lõksu, kust neid on võimalik selektiivselt, kindla mass-laengu suhtega, väljutada, kasutades RF ja DC elektriväljade lühiajalisi skaneerimisi.

Eelised:

Suurim massi-lahutusvõime kõikidest mass-spektromeetritest.

Head võimalused viia läbi ioon-keemia ja mass-spektromeetria eksperimente.

Mittepurustav ioonide detekteerimismeetod; ioonide uuestimõõtmise võimalus; NB! Samas võimalik suuri molekule “tükeldada”

Lennuaja-spektomeetria: TOF-SIMS

Lennuaja-spektromeetrias mõõdetakse detektorisse jõudnud objektilt hajunud osakeste voogu primaarioonide pulsist mõõdunud aja (lennuaja) suhtes:

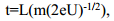
kus, t- iooni lennuaeg objektist detektorini, Lvahemik objektist detektorini, U- kiirendav pinge ja m/e- uuritava iooni mass-laengu suhe.

Reeglina katab sekundaarsete ioonide energia mingit vahemikku, mis tekitab kindla massimääramise vea. Viimast saab vähendada ioone korduvalt edasi-tagasi peegeldades spetsiaalsete elektrostaatiliste peegeldajate abil. See pikendab ühtlasi ka ioonide lennu teepikkust ning parandab sellega ka spektromeetri massilahutust.

Spektromeeter vajab pulseerivat ioonide allikat, milles “kiir peal” aeg on palju väiksem “kiir kinni” ajast, tüüpiliselt 20-250 ns 10-20 kHz kordamise sageduse juures (50-100 µs) – seade vajab suhteliselt kiiret elektroonikat.

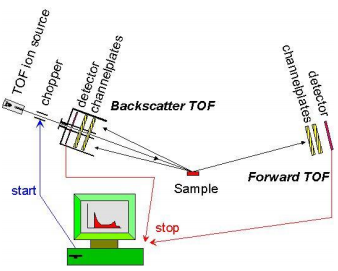Spektromeetri eelised on suur mõõdetavate ioonimasside vahemik, hea sekundaarioonide “ärakasutamine”, seega ka tundlikkus.

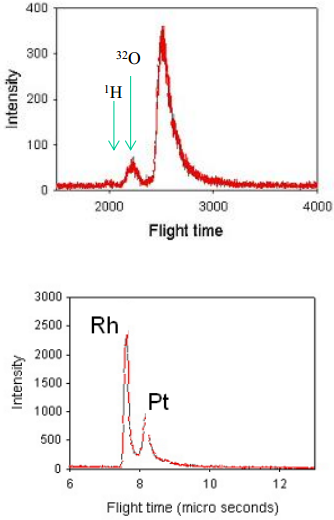Otsehajunud või tagasipeegeldunud osakesi detekteeriv geomeetria võimaldab mõõta, vastavalt, kergeid (NB! ka H) ja raskemaid (alates Ti) elemente.

Ülemine graafik näitab objekti Pt₂₅Rh₇₅(410) pinnalt otsehajunud ioonide spektris ülinõrka H põrkepiiki (recoil peak; ~2000 suht. ühiku juures), nõrka O põrkepiiki ~2200 juures ja laia, põhilist hajumispiiki ~2600 ühiku juures. Seega otsehajunud spekter on tundlik kergetele elementidele ja näitab pinnakihi saastumist kergete elementide-ühenditega. (Scattering And Recoiling Spectroscopy (TOF-SARS)).

Alumisel, kalibreeritud graafikul on toodud sama objekti tagasipeegeldunud ioonide spekter, kust näeme maatriksi põhikomponentidele vastavaid piike.

SIMS-mikroskoopia

(Nt O isotoopide mõõtmine)

21. Ioonide hajumise spektroskoopia: jaotus ioonkimbu energiate järgi;

Kui ioonsond suunata objekti pinnale, siis teatud osa ioone peegeldub/hajub sellelt elastselt tagasi. Nende hajunud ioonide intensiivsuse sõltuvus peegeldusnurgast annab informatsiooni pinna kristallograafilise struktuuri kohta. Siin baseerutakse ioonide hajumisteooriale, mis võimaldab leida aatomite asukohad pinnal. Keerukamaks teeb selle teooria rakendamise asjaolu, et pinna purustuste vähendamiseks ioonidega pommitamisel tuleb kindlasti kasutada väikese energiaga ioone (E<5 keV), selliste ioonide puhul aga pole laengu neutraliseerimise efektid seni hästi mõistetavad. Samas tuleb arvestada ka võimalike pinnale adsorbeerunud ioonide mõjuga, mis olemasolul varjutavad originaalseid pinna-aatomeid. Sageli kasutatakse ioonspektromeetriat pinnakihtide elemendiliseks analüüsiks, mida vaatleme järgnevalt põhjalikumalt.

Primaarioonide energiate järgi jagatakse ioonide hajumise spektroskoopia (ISS, ion scattering spectroscopy)

madalaenergeetiliste ioonide hajumiseks (LEIS) 1-10 keV

keskmise- (MEIS) 20-200 keV

kõrge- (HEIS) 0.2-2 MeV energiaga ioonide hajumiseks

Rutherfordi tagasihajumise spektromeetriaks (RBS), 2-3 MeV.

Heilandi skeem ja valem madala energiaga ioonide hajumisel.

Heiland’i järgi madala energiaga inertgaasi ioonide kiir, osakeste massiga M₁ ja energiaga E₀, langedes tahkise pinnale, mis koosneb aatomitest massiga M₂, peegeldub sellelt elastselt ning hajunud kiire ja primaarkiire vahelise nurga Θ puhul, hajunud kiire osakeste energia avaldub seosega:

Siin märk + kehtib kui M2/M1>1, ja vastupidi.

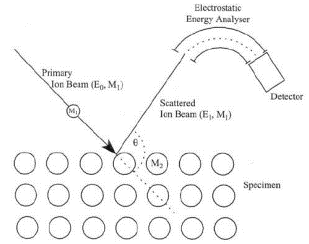
Samas, kui Θ=π/2, saame eelnevast seosest tuletada seose pinna-aatomite massi määramiseks:

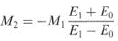
Seega, mõõtes E₁ ja teades E₀ ja M₁, saame määrata M₂.

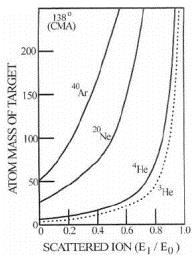Madalaenergeetiliste He-, Ne- ja Ar-ioonide alg ja lõppenergiate vaheline sõltuvus hajumisel tahkise pinnalt (Θ=138^o).

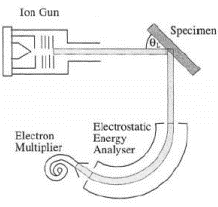
Madala ja keskmise energiaga (E0<50 keV) ioonide hajumise katseseade koosneb ioonkahurist, vaakum-objektikambrist ja ioonide energiaanalüsaatorist koos vastuvõtjaga. Joonisel on toodud elektrostaatiline energiaspektromeeter, see võib olla ka magnetiline või kombineeritud, sisaldades mõlemat tüüpi spektromeetreid. Seega kuulub selline seade laboratoorsete seadmete klassi.

Rutherfordi tagasihajunud ioonide spektromeetria: hajumisskeem;

Rutherford tagasihajumise spektromeetria (Rutherford backscattering spectrometry , RBS) puhul mõõdetakse objektilt tagasipeegeldunud α-osakeste (radioaktiivsel lagunemisel tekivad) energiat. Nende osakeste energia sõltub aatomitest, millelt nad tagasi hajuvad ning sügavusest kus need aatomid asuvad ja hajumisnurgast. Seega saab RBS-i kasutada objekti pinnalähedase ala elementanalüüsiks.

Suur osa objekti pommitavatest osakestest implanteeritakse pinnakihti, kuna aatomi tuuma mõõde on suurusjärgus 1e-15 m ning aatomtasandite vahekaugus ~2e-10 m. Mõned osakesed, mis kohtuvad objekti aatomite tuumadega, hajuvad viimastel eri suundades.

Kindla nurga all tagasihajunud osakeste energia sõltub kahest protsessist:

osakesed kaotavad energiat objektis liikudes, nii enne, kui pärast põrkumist, põhiliselt interaktsioonis aatomite elektronkatetega. Seda energiakadu iseloomustab antud aine pidurdusvõime (ingl.k. stopping power),

osakesed kaotavad energiat ka põrkeprotsessil.

Siin on tegemist positiivselt laetud osakeste kulonilise vastastikmõjuga, mille tagajärjel toimub elastne põrkumine- impulsside muutus. Seega osakese energiakadu põrkel sõltub osakeste masside suhtest. Energiate suhet, mis osakesel oli enne ja pärast põrget nimetatakse kinemaatiliseks faktoriks (ingl.k. kinematic factor). Kindla elemendi aatomitelt hajunud osakeste arv sõltub nende aatomite kontsentratsioonist ning nende tuumade efektiivsest suurusest, mida iseloomustab antud aine hajumise ristlõige (ingl.k. scattering cross section).

kasutatavad ioonid ja nende energiaväärtus;

kasutatakse ¹H₁, ²He₄, ³Li₇ ioone, energiaväärtused: u 0,5-2,5 MeV

hajumisristlõige sõltuvalt elemendi järjekorranumbrist;

Tõenäosus, et osake hajub kindlas ruuminurgas Θ, avaldub hajumise ristlõike seosega:

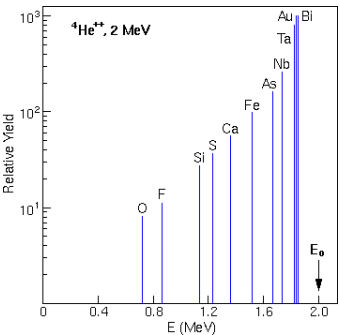Hajumise ristlõige on võrdeline pommitatava aatomi massi ruuduga. Seda illustreerib kõrvalolev graafik. Ühtlasi näitavad horisontaaltelje energiad kujukalt suurt osakeste energiamuutuse erinevust hajumisel kergetelt (ning väikest rasketelt) aatomtuumadelt.

pidurdusvõime;

Osake, mis põrkub märklaua aatomilt objekti sügavuses, omab tunduvalt väiksemat energiat, kui osake, mis põrkub märklaua sama elemendi pinnalähedase aatomiga. Osakese energiakaotus on põhjustatud eelkõige selle interaktsioonist märklaua aatomite elektronidega (elektronpidurdus) ja osakese põrkumistest märklaua aatomitega väikeste nurkade all (tuumapidurdus). Energiakogus, mille pommitav osake kaotab oma teekonnal objektis sõltub osakeste liigist, selle kiirusest, märklaua elemendilisest koostisest, ja märklauad-objekti tihedusest. Tüüpiliselt on 2 MeV algenergiaga He-ioonide energiakaod vahemikus 100 kuni 800 eV/nm.

profileerimine – hajumisspektrite seletus.

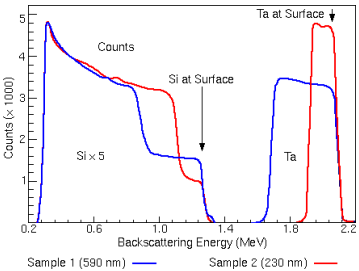
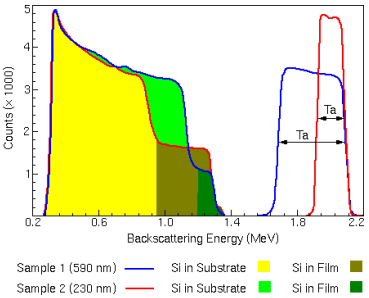See, osakeste energiakadude sõltuvus objekti koostisest ja tihedusest, võimaldab RBS mõõtmiste abil määrata kilede paksusi, s.o. viia läbi sügavuse järgi profileerimist. Kõrvalolev graafikul on toodud osakeste, algenergiaga 2.2 MeV, energiajaotus pärast hajumist Sialusele kasvatatud TaSi-kiledelt. Kõrgenergeetilised jooned on põhjustatud osakeste hajumisest Ta-aatomitelt, madalaenergeetiline spekter aga Si-aatomitelt, sealjuures on viimane suurendatud 5x (kergetelt aatomitelt hajumise ristlõige on väike, vt. eelmine joonis). Ta-silitsiidis on Si-aatomite kontsentratsioon väiksem, kui puhtas Si-s. Seetõttu on kiles Siaatomitelt hajumine väiksem, kui Si-aluses. Samas kaotavad osakesed enne Sialuseni jõudmist tuntava osa oma algenergiast, seetõttu on ka aluse pinnalt hajunud osakeste energia väiksem, kui kile Si-aatomitelt hajunud osakeste energia.

Mõõtes Ta-joone (või Si-astangu) energeetilise laiuse ja jagades selle He-ioonide energiakaoga osakese teepikkuse ühiku kohta Ta_xSi_y-s, saame kile paksuse. Nii mõõdeti õhema kile paksuseks 230 ja paksemale 590 nm (tihedus 9.14 g/cm³). Siinjuures tuleb arvestada, et osakeste energiajaotus laieneb nende objekti sügavusse tungimisel. See põhjustab paksu kihi korral alusepoolse spektriosa laienemise (ingl. k. straggling), mis tuleb arvesse võtta kile paksuse ja üleminekukihtide olemasolu määramisel. Kile koostis määratakse hajumisspektrite kõrguste järgi, võttes arvesse osakeste hajumise ristlõiget eri ainetes. Näiteks on osakeste hajumisristlõige TaSi₂-s 1.37 korda suurem, kui puhtas Si-s. Seega on näiteks TaSi₂-s (aatomite suhe 2:3) Si-piik vaid 0.487 puhta Si-piigist.

RBS ja TOF-ERDA võrdlus.

RBS

Rasked elemendid kergemates objektides – kasutades ¹H^1-, ²He^4-, ³Li^7- ioone

TOF-ERDA

Time of fligt elastic recoil detection analysis

Kerged elemendid rasketes objektides – kasutades raskemate elementide ioone (¹⁷C₃₅, ⁵³I₁₂₇)

Probleemküsimused: Objektis on vaja mõõta OH- ja COOH-rühmade olemasolu, millise meetodiga neid määrata, kui IR-spektromeetriat ei saa rakendada? Kuidas profileerida P-lisandi jaotust Si-kristalli pinnalähedases ruumis, kui objekti pihustamine pole lubatud? Milline kursuses käsitletud analüüsimeetod on kõige tundlikum väikeste lisandkoguste detekteerimiseks? Vajalik on uurida W-oksiidi õhukese kile mittestöhhiomeetriat, millist (milliseid) ioonspektromeetria meetodit (meetodeid) te kasutaksite – põhjenda valikut

Tundmatu meteoriit: milline on meteoriidi koostis ja elementide jaotus? Isotoopide jaotus lihvitud alal? Kas objekt on kristalliline? Kas ja millist objekti ettevalmistamis on vaja kasutada?

Elementide jaotuse uurimine, mis ei oleks nii destruktiivne kui SIMS; x-rayga kiiritame, saame fotoelektrone (fotoelektronmikroskoopia, skaneerimine – liigutatakse proovi

Simsiga või fotoelektronidega (või Auger elektronidega) meetodid on suht lokaalsed (100x100um)

XRF’ga kaardistamine fotoelektronmikroskoopia – valime koha, kus on must ja valge ala kõrvuti; peenstruktuuri uurimiseks Auger elektronmikroskoopia juurde; objekti ettevalmistades, saab TEMiga uurida

Metalliline meteoriit? OM’ga midagi teha pole; SEM, XRF (mapping) – saab millimeeterlahutuse; peenemasse lahutusse minnes on vaja väga paljudest kohtadest mõõta, et mingit keskmist saada

Kristallstruktuuri jaoks: XRD-ga

Kihiline paksem materjal: pealmine kiht u 10 um paksune komposiitmaterjal (mitme mikromeetrised terakesed), alumine kiht 100 um paksune komposiit; amorfne materjal

Kuidas uurida koostise jaotust erinevates pinnakihtides? Pinna määramine: ioonmeetod, simsiga miksoskoppia, saame uurida 20x20 um ala peal, kuidas asjad jaotunud

Keskmise ala uurimiseks – murrame puruks, lihvime nt, siis saame ka kaardistada; kui raha liiga palju, siis teeme simsiga kraatri, kaardistame seda minnes aina sügavamale, minnes isegi materjalist läbi, sest 100 um pole liiga paks ala; mida sügavamale läheme, siis seda karedamaks asi läheb, seda kehvem lahutus; kui teeme kraatrit, siis äärest ei mõõda, mõõtmine käib keskel (3D mikroskoopia)

Kui on 10 um ja teisel pool veel 100 um, siis koostise ja paksuse uurimiseks mõistlik kasutada SEMi (100um küljelt vaadates, väga hästi tuleb välja, 10 um läbi uurida ka väga lihtne) < see vastus eksami jaoks; 10 nm juhtival materjalil SEMiga ok (vahekihi määramiseks on kehv variant, midagi näeb, aga x-ray interaktsiooniruumala nii suur, et lahutus kehv)

Kuidas määrata täpsed kihtide paksused ning mikroskoopiliste komposiitmaterjalide osakeste suurus?

Kahe erineva kristallpulbri uurimine, need kokku segatud ja paagutatud

Kas osakesed ühtlaselt jaotunud? Läbivalgustav elektronmikroskoop; ettevalmistus: TEMile vaja hästi õhukest kihti, kui kildudeks teha, siis servast saab uurida osakeste jaotust ja suurust

Kui suured osakesed?

Kuidas on osakesed omavahel liitunud? (st kuidas aatomid kahe osakese ühinemiskohas ühinenud on, /STEMi jaoks liiga kare, SIMSiga liiga väike lahutus/; TEMiga otsid kõrglahutusega selle vahepealse osa üles ja katsud uurida sed

Objekti ettevalmistamine: purustamiseg prepareerimine kehv variant (kilde tehes); peaks lõikama, aga enne seda peaks poorid täitma mingi polümeeriga, sest kiibiga lõigates ei saa väga head lamelli pinda, sest pooride kohast need ioonid lähevas ügavusse ja kõrgematest kohtadest hakkab lõikama ja kannab materjali pooride põhja ja seetõttu on see raske objekt üldse prepareerimiseks; kui poorid täidetud, siis saab kiibiga väga hästi lõigata

Makrsokoopilise objekti (100x100 um) üldise jaotuse määramine – SEM

Saab määrata ära tera suuruse, aga kas see on osakese suurus, seda ei saa; kui tegu kristallilise objektiga, siis võivad appi tulla difraktsioonilised meetodid (joone laienemine) või kõrglahutusega TEM, kus näeb osakese struktuuri ja saab erineva kristallorientatsiooniga kristalliitide suurused kätte; kui pole kristalliline, siis on problemaatiline, mingil määral võib TEMiga mappingut tehes näha jaotust.

Grafeen

Millist meetodit kasutada, er näha 6-st C aatomist koosnevat rõngast

Tuneelmikroskoppia; vaja teravikke (kuidas neid ettevalmsitada? Traadist tõmbamine, KOHga söövitati ja saadi hästi terav ots

Objekti ettevalmistus: juhtivale pinnale kinnitame

STEMis: proov positiivne, teravik negatiivne või vastupidi

Aatmojõu mikroskoobid võimaldavad ka aatomlahutust, kui objekt tasapinnaline

STEM kõige parem variant, siis AFM selle materjali jaoks

Mitmekihiline objekt on? Kui nt on 3 kihti üksteisi peal. Kui astanguid ei ole, siis teravikmikroskoopiaga ei saa (SEM ei anna aatomlahutust); TEMiga uurida nt, siis proovi ettevalmistus: peame vaatama risti seda objekti, st et näeks neid kolme kihti külje pealt

STEMiga saab määrata väga hästi, kas tegu 1 või 2-3 kihilise grafeeniga; pm võiks isegi näha, kuidas aatomid reas üksteise suhtes paigutunud on; kui täiesti 1-kihiline grafeen, siis saame kindlasti kõik aatomid fikseeritu STEMi pildis; STEMiga näeme elektrontiheduse jaotus, seal, kus kaks aatomit üksteise kohal, siis näeme oluliselt paremini kui seal, kus on ainult 1 aatomkiht

AFM 1. küs eelviimane osa

Skaneerimine vs mehaaniline skaneerimine

Lühendid: STEM, STM, TEM, AFM, OM, SIMS, SIMS-MIKROSKOOPIA, ISS, RBS, EELS (electron energy loss spectroscopy), XPS, PES UPS, ESCA, SPEM, AES, AEM, XRD, XRR, EDS, FIB

AFM- pioesoelektriline skaneerimine, STEM – mähistega

Pöördvõre ja reaalvõre: iga difraktsioonipunkt tekib mingi kindla võretasandi difraktsioonist

Võrdle OM ja TEM

Elektronid keerlevad spiraalselt ümber optilise telje – magnetläätses hakkabki elektron spiraalikujuliselt liikuma (SEMis tomib ka see sama asi), pm kujutis on keeratud mingi nurga võrra kujutatava objekti suhtes (SEMis see keeratakse tagasi, et saaks üks ühele vastavuse)

Tunnelvool: lokaalsed olekutihedus; mida mügarused tähendavad (joonis tunnelmikroskoopia juures slaidil lokaalne olekutihedus); tähistavad täidetud ja täitmata olekuid pm pinnakihi aatomite kohta; tahetakse näidata, kuidas

Täidetud olek: see, kuhu enam elektrone juurde ei mahu; Täitmata olek: elektrone mahub veel juurde; seotud juhtivus - ja valentstsooniga

Fotoelektrilise efekti seletamine energiadiagrammidega: XPSjaAES slaid 3 ilmselt, fotoefekt, karakteerse x-ray teke, auger elektroni teke (järjestus slaidil vasakult paremale)

51